2020/04/03 - [AI/Math] - 확률의 기본 용어 정리 (experiment, sample space, event, atomic event)
확률의 기본 용어 정리 (experiment, sample space, event, atomic event)
집합과 확률의 관계 집합에 대해서는 아래의 글에서 정리해뒀다. 이번글에서는 확률의 기본적인 용어에 대해서 알아 볼 것이다. 2020/03/22 - [AI/Math] - 집합 총 정리(set, element, subset, filtering, univers..
supermemi.tistory.com
앞의 글에서 확률의 기본 용어들에대해 정의 했다.
이번에는 확률의 법칙에 대해서 알아 보겠다.
Probability Laws
Probability laws란 어떤 events A ⊆ Ω 에 대하여 0 ~ 1 사이의 숫자를 부여하는 것이다. ( 0 ≤ P(A) ≤ 1)
P(A) 가 1에 가까울 수록 events A가 일어날 가능성이 높은 것이고, 0에 가까울 수록 가능성이 낮은 것이다.
Probability Axioms
-
Nonnegativity : P(A) ≥ 0 for every A, 확률값은 항상 0보다 크거나 같다.
-
Normalization : P(Ω) = 1, 전체 집합의 확률값은 항상 1이다.
-
Additivity : P(A ∪ B) = P(A) + P(B) if A and B are disjoint, A와 B가 서로소집합일때 합집합의 확률은 각 확률을 더한 것과 같다.

Properties of Probability Laws
-
If A ⊆ B, then P(A) ≤ P(B)

-
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
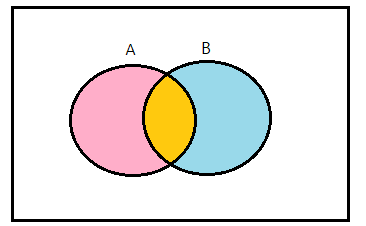
-
P(∅) = 0
-
P(A^c) = 1 - P(A)
-
P(E ∩ F) ≥ P(E) + P(F) - 1
Procedure : P(E)
-
전체 결과의 개수를 찾는다. |Ω|
-
Atomic event O를 찾고, P(O)를 개산한다. 만약, 결과가 모두 같은 확률이라면, P(O) = 1 / |Ω|
-
Event E 를 atomic event의 합집합으로 표현한다.
-
P(E)를 계산한다.
P(E) = P(O_1 U O_2 U ... U O_n) = |E| / |Ω|
다음은 Discrete Uniform & Conditional Probability 에 대해서 알아 보겠다.
이산 균등 확률 & 조건부 확률은 무엇인가? (Discrete Uniform Probability & Conditional probability)
기본적인 용어를 잘 모르겠다면 아래의 글을 보고 오길 바란다. 2020/04/03 - [확률과 통계] - 확률의 기본 용어 정리 (experiment, sample space, event, atomic event) 확률의 기본 용어 정리 (experiment, samp..
supermemi.tistory.com



