[ 확률과 통계 ] 이산 균등 확률 & 조건부 확률은 무엇인가? (Discrete Uniform Probability & Conditional probability)

기본적인 용어를 잘 모르겠다면 아래의 글을 보고 오길 바란다.

2020/04/03 - [확률과 통계] - 확률의 기본 용어 정리 (experiment, sample space, event, atomic event)

확률의 기본 용어 정리 (experiment, sample space, event, atomic event)

---

1. Discrete Uniform Probability Law

 

 

•  만약 sample space Ω 가 유한하고 모든 결과가 동일한 확률을 가질때, P(A) = | A | / | Ω | 이다.

 

 

앞서 배운 atomic event의 disjoint 성질을 이용하면 된다.

 

  -  Event A = {O_1, O_2, ..., O_n } , size = | A | = n

 

  -  P(O_i) = 1 / | Ω |    <- 모든 결과가 동일한 확률을 가지기 때문이다.

  -  P(A) = P (O_1 U O_2 U ... U O_n)     <- 서로 disjoint set 이다.

        = P(O_1) + ... + P(O_n)

        = n X (1/| Ω |)    <- n개가 있음.

 

---

예시 1 ) 주사위 굴리기.

 

sample space Ω  =  discrete    { 1, 2, 3, 4, 5, 6}

out comes  =  uniform    1 / 6 ( = 1 / | Ω |)

Event A  =  주사위의 수가 짝수이다.

 

A  =  {2, 4, 6}

P(A)  =  | A | / | Ω |  =  3 / 6  =  1 / 2

 

---

예시 2 ) 4면 주사위 2개 던지기. 주사위의 결과는 공평하다.

 

sample space Ω  =  discrete    { (1,1), (1,2), ... , (4,4) } - 16가지의 경우.

out comes  =  uniform    1 / 16 ( = 1 / | Ω |)

Event E  =  A (주사위의 합이 5보다 크거나) U B (첫번째 주사위가 2일 경우)

    P(E) = P(A) + P(B) - P(A ∩ B)

          = ( 6 / 16 ) + ( 4 / 16 ) - ( 1 / 16 )

          = 9 / 16

 

그림으로 그려보면 이해가 쉽다.

A  =  { (2,4), ..., (4,4) }  :  PINK + PURPLE

B  =  { (2,1), (2,2), ..., (2,4) }  :  SKY + PURPLE

A ∩ B  =  { (2,4) }  :  PURPLE

---

2. Conditional Probability

 

조금 햇갈릴 수도 있다. 집중해서 보자!

 

말 그대로 조건이 있는 상황에서 확률을 추론해 보는 것이다.

 

 

 

•   먼저 사건은 이미 일어 났다.

•   그리고 우리는 그 사건의 부분적인 정보만을 안다.

•   그때 event A 일 확률을 구하는 것이다.

•   P( event | partial information )

•   P(A | B) = P(A ∩ B) / P(B)   ( Assuming P(B) > 0 )

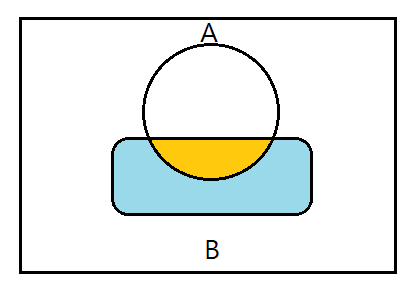
•   Conditional probability Axiom  :  Additivity 

  • (if A_1, A_2 disjoint)   P(A_1 U A_2 | B) = P(A_1 | B) + P(A_2 | B)

 

---

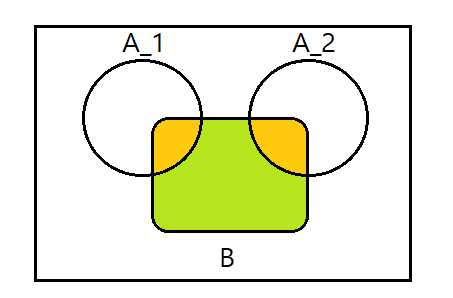
위와 똑같은 상황의 예시를 통해 설명하겠다.

 

예시 1) 주사위 굴리기.

 

주사위는 이미 던져 졌고, 그 결과 주사위의 눈은 짝수라는 것을 안다.

이때, 결과가 6일 확률은 얼마가 되는가?

 

위의 문장을 잘 읽어보고 차근차근 정리 해보자.

일단 결과가 홀수일 확률은 아예 없다. 왜냐하면 부분적 정보로 짝수라는 것을 알려줬으니!

그렇다면 결과가 6일 확률은 1 / 3 이 된다고 추론 할 수 있다.

 

Event A = { 6 }

부분적 정보 B = 짝수 { 2, 4, 6 }

 

    P(A | B) = P(A ∩ B) / P(B)

               = (1 / 6) / (3 / 6) = 1 / 3

 

---

예시 2 ) 4면 주사위 2개 던지기. 주사위의 결과는 공평하다.

 

주사위를 던졌다.

그 결과의 합이 5보다 클 때, 첫번째 주사위의 눈이 2일 확률을 구해라.

 

sample space Ω  =  discrete    { (1,1), (1,2), ... , (4,4) } - 16가지의 경우.

out comes  =  uniform    1 / 16 ( = 1 / | Ω |)

 

Event A  =  첫번째 주사위가 2일 경우   =   { (2,1), ..., (4,4) }  :  PINK + PURPLE

부분적 정보 B = 합은 5 보다 크다   =   { (2,1), (2,2), ..., (2,4) }  :  SKY + PURPLE

A ∩ B = { (2, 4) }  :  PURPLE

  P(A | B) = P(A ∩ B) / P(B)

             = (1 / 16) / (6 / 16) = 1 / 6

---

다양한 예제 문장

 

1.  P( A U Ω ) = 1

2.  0 < P(B) < 1,   P(A ∩ B) ≤ P(A/B)

3.  (A^c U B^c) = (A ∩ B)^c

4.  If A and B are disjoint events than P(A U B) = P(A) + P(B)  by additivity axiom

5.  P(A U B) ≤ P(A) + P(B)

6.  P(A_1 ∩ A_2 ∩ ... ∩ A_n) ≥ P(A_1) + ... + P(A_n) - (n-1)

 풀이

 

1 - P(A_1 ∩ A_2 ∩ ... ∩ A_n)     =     P( (A_1 ∩ A_2 ∩ ... ∩ A_n)^c )

P( (A_1 ∩ A_2 ∩ ... ∩ A_n)^c )   =     P(A_1^c U A_2^c U ... U A_n^c) 

P(A_1^c U A_2^c U ... U A_n^c)  ≤     P(A_1^c) + ... + P(A_n^c)  =

P(A_1^c) + ... + P(A_n^c)           =     (1 - P(A_1)) + ... + (1 - P(A_n))

↓

1 - P(A_1 ∩ A_2 ∩ ... ∩ A_n)     ≤     n - (P(A_1) + ... + P(A_n))

 

그림 출처

https://timewithai.com/2019/07/19/conditional-probability-and-independence-introduction/