[ Math ] Four-quadrant Inverse Tangent (Arctangent) Function
일반적으로 학교에서 sin(사인) cosine(코사인) tangent(탄젠트)가 무엇인지
즉, 삼각함수에 대해서 배웠을 것이다
삼각 함수 미분 공식 & 그래프.
여러가지 형태에 대해서 미분하는 방법들은 앞서서 다뤘다. 2020/04/12 - [AI/Math] - [미적분] 여러가지 미분 공식과 예제 (Chain rule, Power rule, sum/difference rule, Exponential functions, Product rule,..
supermemi.tistory.com
그리고 이러한 삼각함수의 역함수를 각각 arcsin arccos arctan 라고 부른다
삼각함수의 역함수의 미분 & 그래프 (arcsin, arccos, arctan)
이전 글에서는 삼각함수의 미분에 대해서 다뤘다. 2020/04/19 - [AI/Math] - [미적분] 삼각 함수 미분 공식 & 그래프. [미적분] 삼각 함수 미분 공식 & 그래프. 여러가지 형태에 대해서 미분하는 방법들은
supermemi.tistory.com
1. Tangent

fig 1. 원에서 보이는 x축과 보라색 직선 사이의 사잇각을 theta라고 할때, tan(theta)의 값은 무엇일까?
아주 간단하다 보라색 직선과 원이 맞닿아 있는 점의 좌표를 (Px, Py)라 할때 fig 2. tangent 처럼 나눠주면 된다.

특정한 theta 값이 아닌 임의의 theta에 대한 tangent graph를 그려보면 fig 3 과 같은 모양이 나온다
하지만 fig 3. tangent graph를 보면 tangent 함수는 주기함수이다
때문에 theta와 one-to-one 관계가 아니다

일반적인 software(MATLAB, atan(X) 함수 )에서는 [-π/2,π/2] 범위에서 값을 return 한다
Inverse tangent in radians - MATLAB atan
You have a modified version of this example. Do you want to open this example with your edits?
www.mathworks.com
2. Arctan
그렇다면 tangent 의 역함수인 arctangent 를 단순히 취하면 어떻게 될까?
정답은 각도가 [-π/2,π/2] 범위에서만 나타나게 된다
fig 4. arctangent 에서 보라색으로 칠해진 영역만 표시할 수 있게 되는 것이다

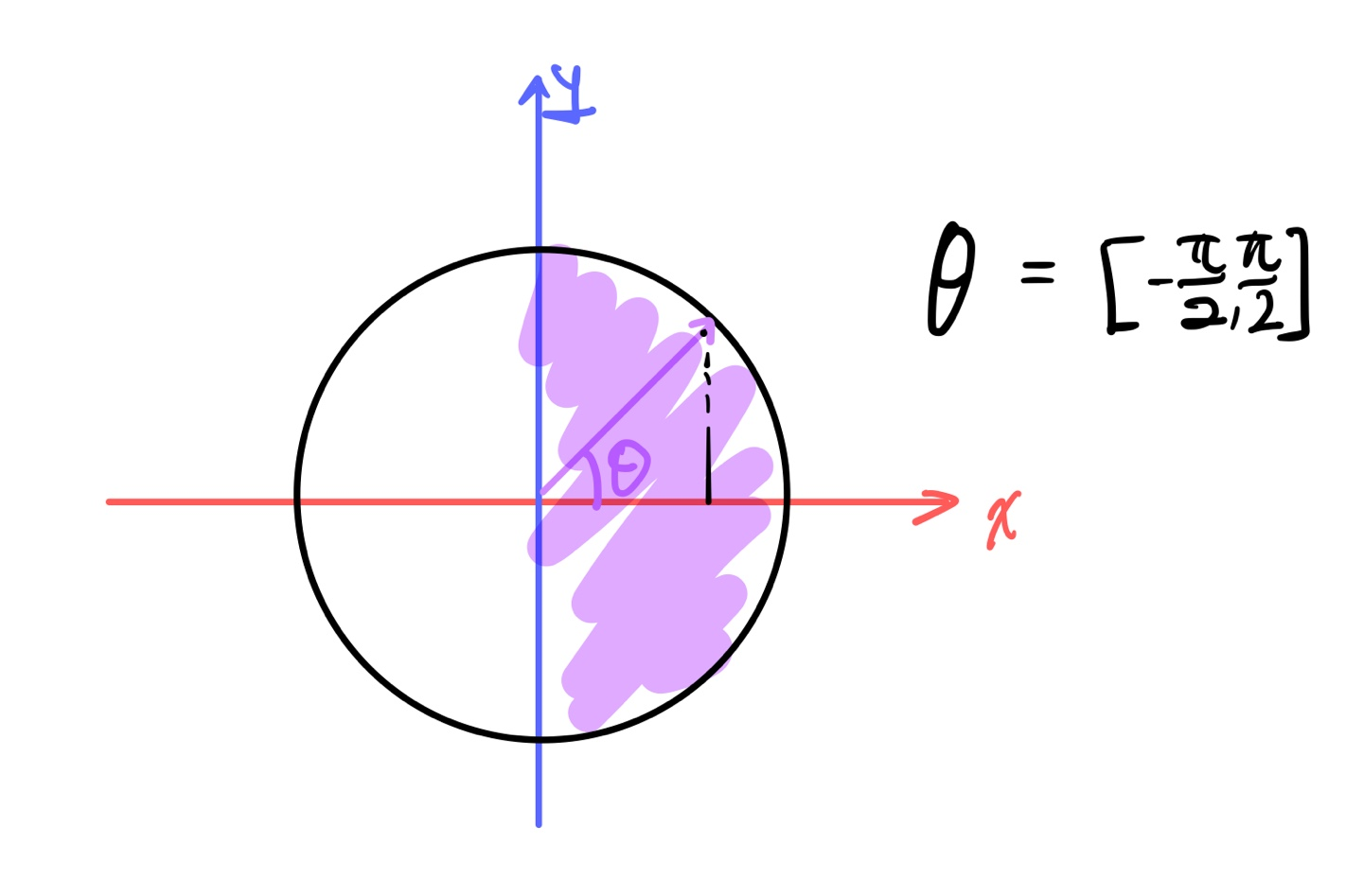
이게 왜 문제일까?
예를 들어 fig 5 에서 alpha 값을 arctangent 로 구할 수 있는가?
Alpha 값은 딱 보기에도 [-π/2,π/2] 범위를 벗어나는 듯하다

이러한 문제를 해결하기 위해 Four-quadrant Inverse Tangent에 대한 내용이 등장한다
3. Four-quadrant Inverse Tangent
점 P를 복소수로 나타냈을 때 다음과 같다.
P = Real + i (Imag)
Matlab 에서 atan2(Imag,Real) 라는 함수로 구현된다
각도의 범위 : [-π ,π]
Y = Imag
X = Real
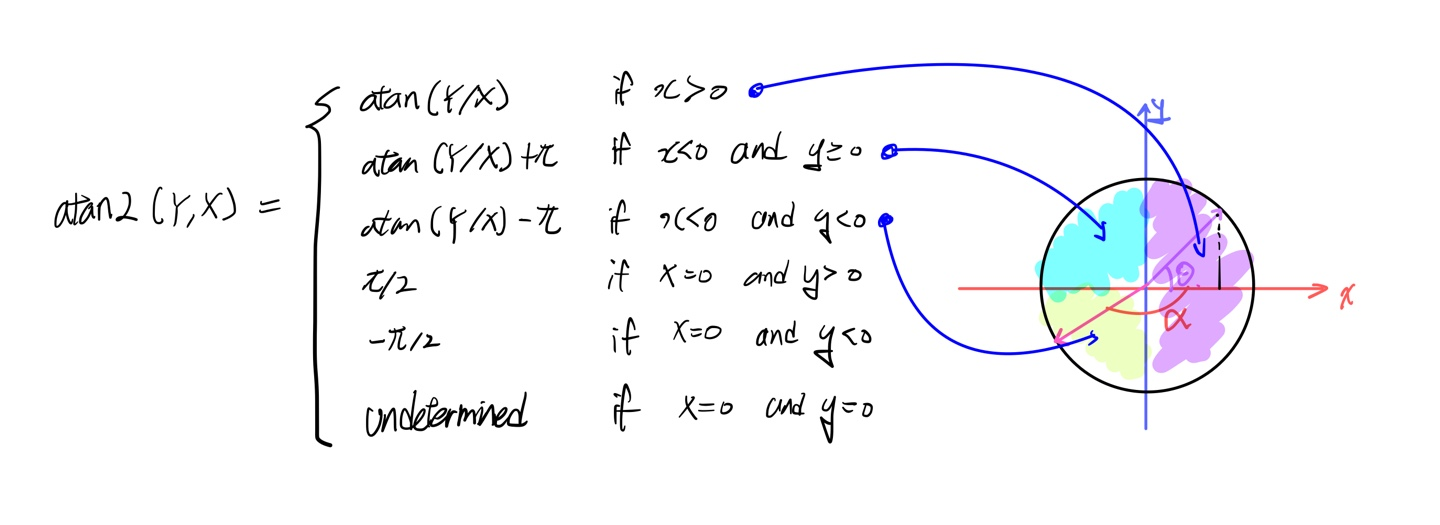
Four-quadrant inverse tangent - MATLAB atan2
The four-quadrant inverse tangent, atan2(Y,X), returns values in the closed interval [-pi,pi] based on the values of Y and X, as shown in the graphic. In contrast, atan(Y/X) returns results that are limited to the interval [-pi/2,pi/2], shown on the right
www.mathworks.com
왜 Four-quadrant inverse tangent 같은 함수를 사용하여 theta의 범위를 [-π ,π] 로 확장 시켰어야 할까?
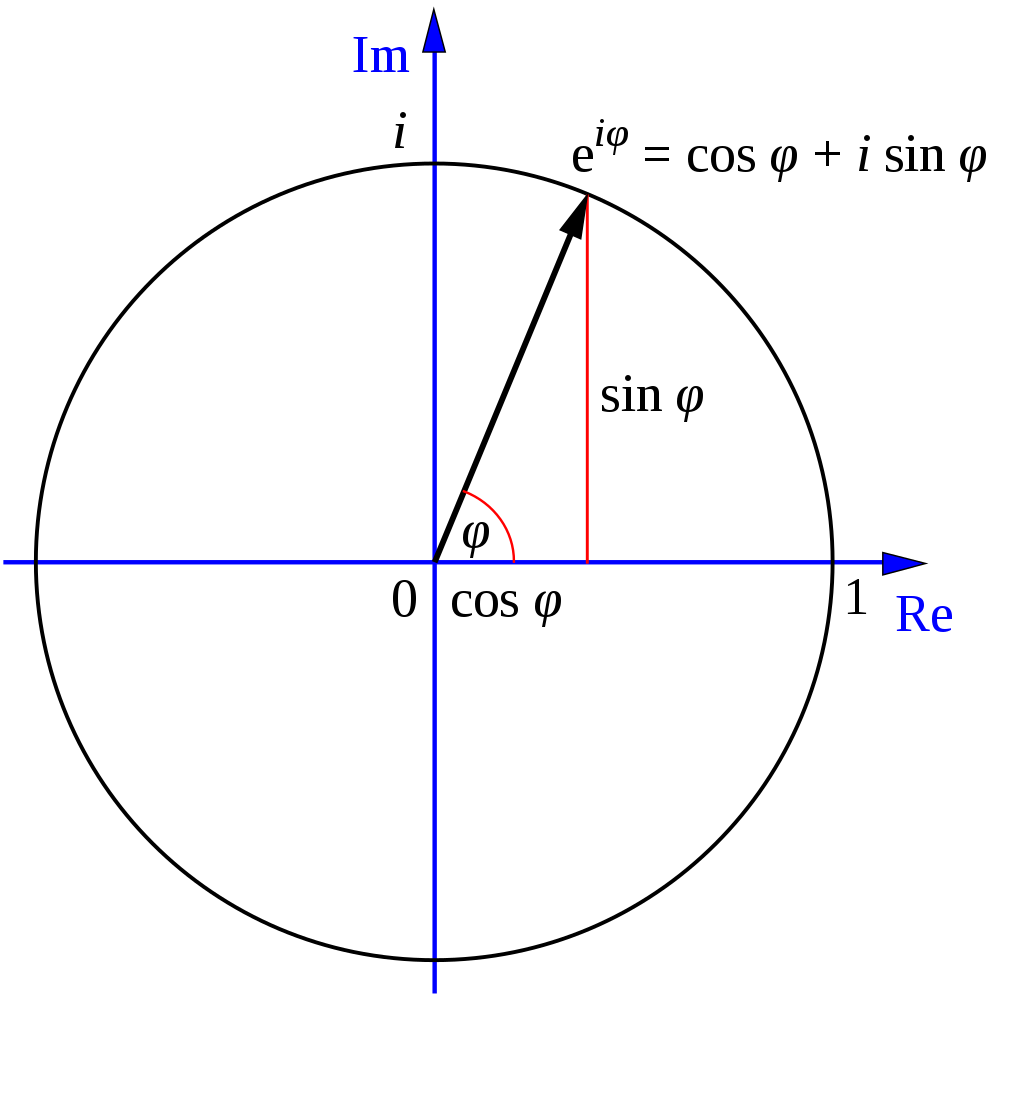
→ 아마도 추측하건데 삼각함수의 주기는 2π 이며 이를 fig 7. 극좌표계(Polar coordinate) 또는 fig 8. 복소평면(Complex plane)에서 적용하기 위함이 아닐까?
위키피디아 극좌표계 설명에서 극좌표를 이용한 점의 표시 부분에서 다음과 같이 설명하고 있다.
"점을 나타내는 방법을 하나로 제한할 때에는 r은 양수로, θ는 구간 [0, 360°) 또는 (−180°, 180°](라디안으로는 [0, 2π) 또는 (−π, π])의 수로 하는 것이 보통이다"

극좌표계 - 위키백과, 우리 모두의 백과사전
여러 각이 표시된 극좌표 극좌표계(極座標系, 영어: polar coordinate system)는 평면 위의 위치를 각도와 거리를 써서 나타내는 2차원 좌표계이다. 극좌표계는 두 점 사이의 관계가 각이나 거리로 쉽게
ko.wikipedia.org
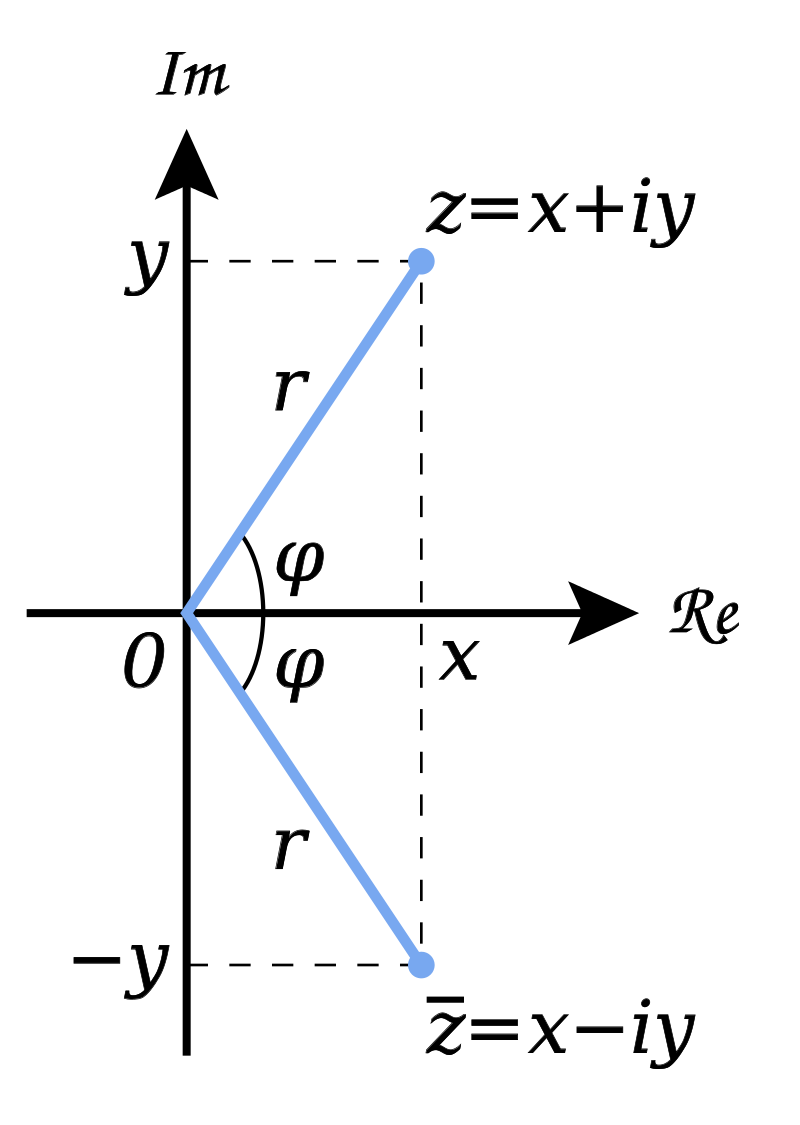
복소평면 - 위키백과, 우리 모두의 백과사전
복소평면에 나타낸 복소수 z와 켤레복소수의 기하학적 표현. 원점에서 점 z를 따라 그어진 파란색 선의 거리는 복소수 z의 절댓값을 나타내고 각 ¢은 z의 논의를 나타낸다. 수학에서, 복소평면(
ko.wikipedia.org
'수학 > Basic' 카테고리의 다른 글
| [ Math ] Convolution(합성곱)의 원리와 목적 (3) | 2021.08.03 |
|---|---|
| [ Math ] Complex Number (복소수) (0) | 2021.07.15 |
| [ 수식, 기호 ] Delta Symbol (델타 : Δ, δ ) (0) | 2021.05.23 |
| 비 유클리드 공간 & 기하학 - 1) hyperbolic geometry(쌍곡 기하학) (2) | 2021.02.08 |
| 유클리드 공간과 기하학 (Euclidean space & geometry) (0) | 2021.02.08 |



