유클리드 공간과 기하학 (Euclidean space & geometry)

유클리드 기하학(Euclidean geometry)이란?

고대 그리스 수학자 유클리드가 구축한 수학의 체계이다.

<<원론>> 에서 2차원의 평면 기하학과 3차원의 공간 기하학등을 다룬다.

19세기 들며 다양한 공간을 정의한 비유클리드 기하학이 만들어지기 시작했다.

유클리드 공간은 중력장이 거의 작용하지 않는 공간에서만 실제 세계와 잘 들어맞는 근사적인 이론이다.

간단히 말하자면 중학교에서 배운 수학의 근본 체계가 유클리드 기하학에 속한다고 생각할 수 있다.

유클리드가 연구했던 평면과 공간을 일반화한 것을 말한다.

이 일반화는 유클리드가 생각했던 거리와 길이와 각도, 좌표계를 도입하여, 임의차원의 공간으로 확장한 것을 말한다.

이는 표준적인 유한 차원, 실수, 내적 공간이다.

만약, 유클리드 공간에서의 거리(distance)에 대해 궁금하다면 다음의 글을 읽고 오길 바란다.

[ Math ] Distance 에 대하여 - 1 ) Euclidean Space

두 점(points) 사이의 거리는 무엇일까? 두 점(points)를 잇는 길(path)의 길이(length)를 말한다. 이때 Euclidean space 라는 공간은 유클리드가 연구했던 평면과 공간을 일반화 한 것이다. 이 일반화는 유클

supermemi.tistory.com

1. 어떤 한 점에서 어떤 다른 한 점으로 선분을 그릴 수 있다.

2. 임의의 선분을 선을 따라 다른 선분으로 연장할 수 있다.

3. 어떤 한 점을 중심으로 하고 이에 대한 거리(반지름)로 하나의 원을 그릴 수 있다.

4. 모든 직각은 서로 같다.

5. 평행선 공준 : 두 직선이 한 직선과 만날 때, 같은 쪽에 있는 내각의 합이 2직각(180도)보다 작으면 이 두직선을 연장할 때 2직각보다 작은 내각을 이루는 쪽에서 반드시 만난다.

위의 공준 5가지가 매우 어려운 말로 쓰여져 있는데, 쉽게 말하자면 일반인들이 생각하는 좌표 평면 세계의 원리 정도라고 보면 된다.

간단한 비교를 위해 다음 그림을 보자.

유클리드 기하학에서는 삼각형의 내각의 합이 180도이다.

다음 글에서 다루겠지만, 비 유클리드 기하학인 구의 표면에서는 삼각형의 내각의 합이 180보다 커지고, 또 쌍곡 기하학에서는 180보다 작아지기도 한다.

이처럼 유클리드 기하학은 좌표가 평면 공간에 위치해 있는 반면, 비 유클리드 기하학은 휘어있는 곡면 공간에 위치해 있다고 볼 수 있다.

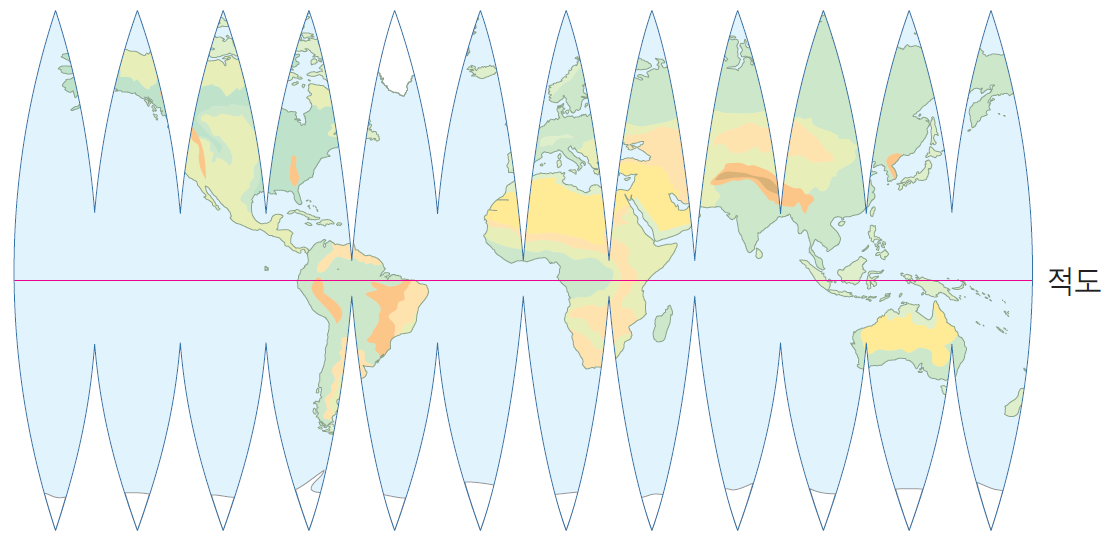
다른 예시로, 지구와 지도를 생각해봐라.

지구는 휜 곡면(Elliptic geometry)에 땅이 위치해 있는데 이를 2차원 평면(Euclidian geometry)로 정확히 표현할 수 없고, 짜른 단면으로 펼쳐서 근사한 것으로 볼 수 있다.

다음 글에서는 비 유클리드 기하학 (non-Euclidean geometry)에 대해서 다뤄 보겠다.

비 유클리드 공간 & 기하학 - 1) hyperbolic geometry(쌍곡 기하학)

앞선 글에서 유클리드 공간과 기하학에 대해서 다루었다. 2021/02/08 - [AI/Math] - [ Math ] 유클리드 공간과 기하학 (Euclidean space & geometry) > 에서 2차원의 평면 기하학과 3차원의 공간 기하학등을 다룬..

supermemi.tistory.com

참고.

[ 수식, 기호 ] Delta Symbol (델타 : Δ, δ ) (0)	2021.05.23
비 유클리드 공간 & 기하학 - 1) hyperbolic geometry(쌍곡 기하학) (2)	2021.02.08
Distance 에 대하여 - 1 ) Euclidean Space (0)	2021.02.08
삼각함수, 쌍곡선함수 공식 총정리 (0)	2020.04.23
쌍곡선함수의 역함수 미분 (arcsinh, arccosh, arctanh) (0)	2020.04.23