앞선 글에서 유클리드 공간과 기하학에 대해서 다루었다.
2021/02/08 - [AI/Math] - [ Math ] 유클리드 공간과 기하학 (Euclidean space & geometry)
[ Math ] 유클리드 공간과 기하학 (Euclidean space & geometry)
유클리드 기하학(Euclidean geometry)이란? 고대 그리스 수학자 유클리드가 구축한 수학의 체계이다. <<원론>> 에서 2차원의 평면 기하학과 3차원의 공간 기하학등을 다룬다. 19세기 들며 다양한 공간을
supermemi.tistory.com
이번 글에서는 비 유클리드 공간과 기하학에 대해서 다뤄 보겠다.
비 유클리드 기하학(non-Euclidean geometry)이란?
비 유클리드 기하학은 유클리드 기하학과 달리 평면이 아닌 곡면의 세계에서 점, 선, 면을 설명하는 것이다.
쌍곡 기하학, 타원기하학 등이 존재한다.
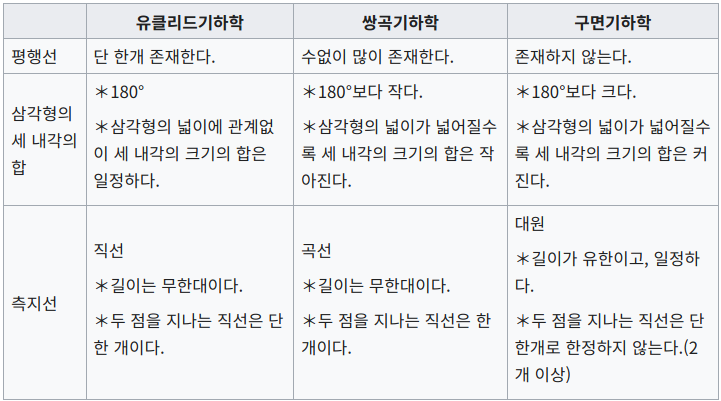
아래의 표를 통해 각각의 기하학적 특성을 비교할 수 있다.

비 유클리드 기하학의 탄생
논리적으로 완벽하다고 믿어왔던 유클리드 기하학의 여러 공리 중에서 평행선 공준에 모순이 있다는 것을 수학자들은 깨닫기 시작했다. 유클리드 기하학은 구부러지지 않은 평평한 면과 공간을 대상으로 하였기 때문에 아무런 문제가 없었지만, 구부러진 곡면과 공간에서는 평행선 공준이 성립하지 않는다. 그 결과 유클리드의 다른 공리들은 모두 받아들여지면서 평행선 공준만을 마꾼 비 유클리드 기하학이 만들어 지게 된다.
1) 쌍곡 기하학(Hyperbolic geometry)
비 유클리드 기하학에서는 공간을 곡률에 따라서 설정한다. 곡률이 0인 공간, 양수인 공간, 음수인 공간으로 구분함으로써 공간을 설명한다.
쌍곡 기하학은 가우스, 로바쳅스키, 볼리아이 등의 수학자들이 만든 기하학으로써 곡률이 음수로 일정한 공간에서 성립하는 기하학으로, 위구 (pseudosphere)와 같은 공간에서 성립한다. 다시 말해, "오목한 면에서 정의되는 기하학"이라고 쉽게 얘기하는데, 정확히는 쌍곡면(Hyperoloid) 위에서 정의되는 기하학 이다.
en.wikipedia.org/wiki/Hyperboloid
Hyperboloid - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Unbounded quadric surface In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principa
en.wikipedia.org
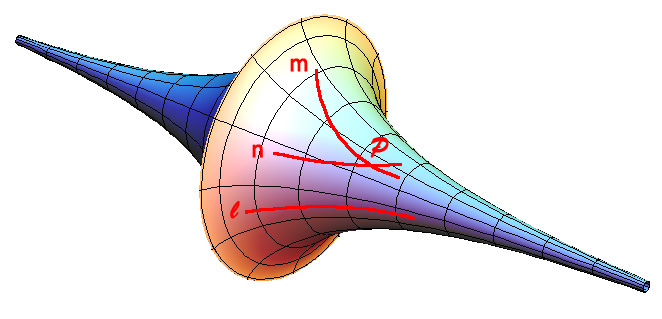
Pseudosphere은 non-Euclidean space의 첫번째 모델 중 하나이며, 표면 전체가 constant negative Gaussian curvature를 따르는 가상의 object를 말한다. 전체를 다 그림으로 표현하기 힘들다. 중심의 원이 끝도 없이 큰 크기를 가지기 때문이다.
이 공간은 양쪽 끝 쪽으로 갈수록 점점 작아져서 그 간격이 0에 가까워진다.
가운데로 갈수록 점점 그 간격이 무한대로 커지는 공간으로, 안으로 휘어진 공간이다.
쉽게 말하면 나팔 두 개를 서로 맞대어 붙여 놓은 것과 비슷한 모양이다.
en.wikipedia.org/wiki/Pseudosphere
Pseudosphere - Wikipedia
In geometry, a pseudosphere is a surface with constant negative Gaussian curvature. Hilbert's theorem says that no pseudosphere can be immersed into three-dimensional space. More detailed description of the pseudosphere[edit] A pseudosphere of radius R is
en.wikipedia.org
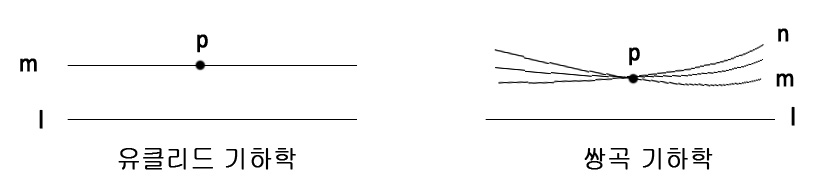
이 공간에서 직선 l과 l위에 있지 않은 점 P가 주어졌을 때 점 P를 지나면서 l과 평행한 직선은 몇 개 일까?
위의 그림에서 보이듯이, 유클리드 기하학에서는 하나의 직선밖에 존재하지 않지만(평행성 공증) 위의 쌍곡 기하학에서는 다양한 직선이 존재할 수 있다.
쌍곡 포물면
namu.wiki/w/%EC%8C%8D%EA%B3%A1%ED%8F%AC%EB%AC%BC%EB%A9%B4
쌍곡포물면 - 나무위키
이 저작물은 CC BY-NC-SA 2.0 KR에 따라 이용할 수 있습니다. (단, 라이선스가 명시된 일부 문서 및 삽화 제외) 기여하신 문서의 저작권은 각 기여자에게 있으며, 각 기여자는 기여하신 부분의 저작권
namu.wiki

기타 hyperbolic geometry 관련 YOUTUBE 설명 자료들
뒤이어, 비 유클리드 기하학의 다른 형태인 elliptic geometry 에 대해 알아 보자.
[참고]
librewiki.net/wiki/%EC%8C%8D%EA%B3%A1_%EA%B8%B0%ED%95%98%ED%95%99
ko.wikipedia.org/wiki/%EB%B9%84%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%EA%B8%B0%ED%95%98%ED%95%99
knun.net/ezview/article_main.html?no=15716
en.wikipedia.org/wiki/Hyperboloid_model
'수학 > Basic' 카테고리의 다른 글
| [ Math ] Four-quadrant Inverse Tangent (Arctangent) Function (0) | 2021.07.14 |
|---|---|
| [ 수식, 기호 ] Delta Symbol (델타 : Δ, δ ) (0) | 2021.05.23 |
| 유클리드 공간과 기하학 (Euclidean space & geometry) (0) | 2021.02.08 |
| Distance 에 대하여 - 1 ) Euclidean Space (0) | 2021.02.08 |
| 삼각함수, 쌍곡선함수 공식 총정리 (0) | 2020.04.23 |



