[ Math ] Convolution(합성곱)의 원리와 목적
Convolution
Convolution (합성곱) 많이들 들어 보셨을 겁니다.
의미적으로는 두 함수를 서로 곱해서 합한다는 것이지요.
합성곱을 공부하셨다면 아래의 질문을 답하실 수 있으신가요?
- 두 함수를 어떻게 곱해서 합하나요?
- 왜 합성곱을 사용하나요? 어떤 역할을 하나요?
하나씩 알아가 봅시다.
두 함수를 어떻게 곱해서 합하나요?
$$ \large (f * g)(t) = \int_{-\infty}^{\infty} f(\tau)g(t-\tau)d\tau $$
두 연속함수 $f, g$를 convolution 하는 식입니다.
이해하셨나요?
먼저, 합성곱을 위해서는 두 함수중 하나를 반전 (reverse)시켜야 합니다.
위의 식을 보면 연속함수 $g$의 변수 타우($\tau$)앞쪽에 마이너스가 붙어있는게 보입니다.
즉 함수 $g$를 반전(reverse) 시켰단 것을 알 수 있네요.
다음으로, 반전시킨 함수를 전이 (shift) 시켜야 합니다.
마찬가지로 함수 $g$ 를 $t$ 만큼 이동 시켰단 것을 알 수 있네요.
마지막으로 이동시킨 함수 $g$를 함수 $f$와 곱한결과를 하나씩 기록합니다.
이때 변수 타우($\tau$)를 변화시키며 결과를 쭉 기록하는 것을 convolution 이라고 합니다!
어떨때는 두 함수가 겹치게 되고, 또 어떨때는 겹치는게 없어서 합쳐도 0이 되기도 합니다.
자 이제 대략적인 개념은 이해했으니 그림을 보며 위의 3가지 순서를 시뮬레이션 해보세요.
하나의 함수($g$)를 반전시킨다. 그리고 이동시킨다.
좌우측으로 옮기며 두 함수를 곱해서 적분한다.
적분을 $\tau$ 에 따라 생각해보면 새로운 모양의 함수형태가 됩니다.
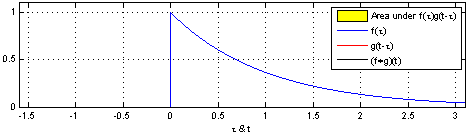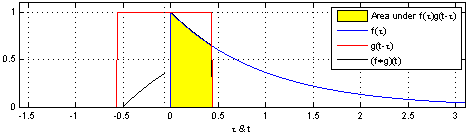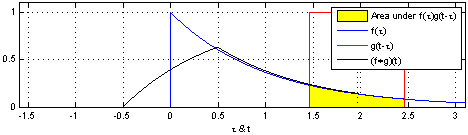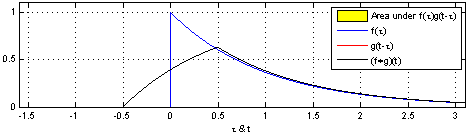
참고로 이산함수 합성곱은 적분(integral)이 아닌 단순 합(summation)으로 표현하면됩니다.
아래 유투버분이 잘 정리해주셔서 구체적인 식이 궁금하시다면 보시는걸 추천드려요
https://www.youtube.com/watch?v=HLYxnTV1N5k&t=1099s
왜 합성곱을 사용하나요?
가장 중요하지만 공부를 하다보면 놓치기 쉬운게 왜? WHY? 인 것 같아요.
공식에만 집중하다 보면 정작 왜 그걸 사용하는지는 잊혀지거든요..
각설하고, 먼저 합성곱은 어디에 사용할까요.
제가 생각해봤을때 행렬의 합성곱(딥러닝), 신호의 필터(샘플링), 라플라스변환, 푸리에변환 등에서 사용되는 것 같습니다.
합성곱 식을 살펴보면 두 함수 $f, g$가 있지요.
일반적으로 사용될때 함수 $f$는 우리가 가지고 있는 본래의 신호, 행렬, 이미지 등이 되기도 합니다.
이때 함수 $g$ 는 필터, 가중치 같은걸로 표현되기도 됩니다.
이 두 함수를 합성곱 하면? 주어진 신호, 행렬, 이미지를 우리가 원하는 함수로 만들어낼 수 있게 됩니다.
즉, 함수 $f$가 주어졌을때 우리가 원하는 목적에 따라 함수$g$를 선정하여 분해, 변환, 필터링 할 수 있다는 장점이 있습니다!
이러한 이유로 합성곱은 다양한 분야에서 활발하게 활용 되는 것이지요.
한가지 예를들어보면, 딥러닝에서 유명한 CNN(Convolutional Neural Network)가 있습니다.
조그만 필터로 이미지를 좌우상하 convolution을 하면서 그 부분의 특징값들을 뽑아내게 됩니다.
입력에 가까울 수록 가장자리(edge), 곡선(curve)과 같은 저수준(low level) 특징을 학습합니다. 출력에 가까워 질 수록 질감(texture), 물체 일부분(object parts)과 같은 고수준(high level) 특징을 인식합니다.
아래 블로그에 정리가 잘 되어 있습니다. 더 궁금하신분은 찾아 보시길..
https://lynnshin.tistory.com/7
[5강] Convolutional Neural Networks
이번에는 Convolutional Layer에 대해 배울 것이다. 먼저 CNN의 역사를 알아보자. <간단한 역사> 1957년 Frank Rosenblatt가 Mark I Perceptron machine 을 개발했다. 이 기계는 perceptron이라고 불리는 알고리즘..
lynnshin.tistory.com
Time domain에서의 합성곱을 잘 설명해놓은 동영상입니다.
다음글
2021.08.04 - [AI/Math] - 푸리에 변환과 합성곱의 관계(Convolution Theorem)
푸리에 변환과 합성곱의 관계(Convolution Theorem)
Convolution(합성곱)의 원리와 목적 Convolution Convolution (합성곱) 많이들 들어 보셨을 겁니다. 의미적으로는 두 함수를 서로 곱해서 합한다는 것이지요. 합성곱을 공부하셨다면 아래의 질문을 답하실
supermemi.tistory.com
'수학 > Basic' 카테고리의 다른 글
| [ Matrix ] 행렬 표기법 정리 (0) | 2022.09.07 |
|---|---|
| [ Math ] Complex Number (복소수) (0) | 2021.07.15 |
| [ Math ] Four-quadrant Inverse Tangent (Arctangent) Function (0) | 2021.07.14 |
| [ 수식, 기호 ] Delta Symbol (델타 : Δ, δ ) (0) | 2021.05.23 |
| 비 유클리드 공간 & 기하학 - 1) hyperbolic geometry(쌍곡 기하학) (2) | 2021.02.08 |



