반응형
[ Matrix ] 행렬 표기법 정리
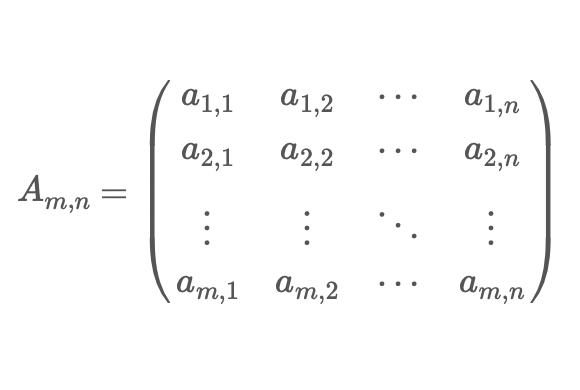
Notation and Nomenclature
- $\textbf{A}$ : 행렬 A → 행렬은 bold 대문자 표현 (중요)
- $\textbf{A}^{T}$ : Transposed 행렬
- $\textbf{A}^{-1}$ : 행렬 A 의 역행렬
- $\textbf{A}^{-T}$ : Transposed 행렬의 역행렬 또는 반대 ($\textbf{A}^{-T}=(\textbf{A}^{-1})^T=(\textbf{A}^{T})^{-1}$)
- $\textbf{A}^{+}$ : 행렬 A 의 Pseudo 역행렬
- $\textbf{A}^{*}$ : Complex conjugated 행렬
- $\textbf{A}^{H}$ : Transposed & Complex conjugated 행렬 (Hermitian)
- $\textbf{A}^{1/2}$ : 행렬의 Square root (unique 할떄), not elementwise
- $(\textbf{A})_{ij}$ = $A_{ij}$ : 행렬의 $(i,j)$ 번째 entry
- $[\textbf{A}]_{ij}$ : $(i,j)$ - submatrix
- $\Vert\textbf{A}\Vert$ : Matrix norm (subscript if any denotes what norm)
- $\textrm{det}(\textbf{A})$ : Determinant of $\textbf{A}$. (행렬식)
- $\textrm{Tr}(\textbf{A})$ : Trace of the matrix $\textbf{A}$. (행렬의 대각합)
- $\textrm{diag}(\textbf{A})$ : 행렬 $\textbf{A}$의 대각 행렬
- $\textrm{eig}(\textbf{A})$ : Eigenvalues of the matrix $\textbf{A}$. (고윳값)
- $\textrm{sup}$ : Supremum of a set. (집합의 상한)
- $A\circ B$ : Hadamard (elementwise) product.( latex : \circ )
- $A\otimes B$ : Kronecker product. ( latex : \otimes )
- $\textbf{0}$ : The null matrix. 모든 요소가 영인 행렬
- $\textbf{I}$ : The identity matrix.
- $\textbf{J}^{i,j}$ : The single-entry matrix. $(i, j)$ 에만 값이 존재하고 나머지는 모두 영인 행렬
- $\bf{\Sigma}$ : A positive definite matrix (Sigma)
- $\bf{\Lambda}$ : A diagonal matrix (Lambda)
- $\textbf{a}$ : 벡터 (column-vector) $\textbf{a}$ → 벡터는 bold 소문자 표현 (중요)
- $a_i$ : 벡터 $\textbf{a}$ 의 $i$ 번째 요소 → 벡터의 요소는 소문자 표현 (중요)
- $a$ : 스칼라(scalar) → 스칼라는 소문자 표현 (중요)
함께 읽어 볼 만한 글
[ LaTeX ] 행렬 표현하기 (matrix, pmatrix, bmatrix, Bmatrix, vmatrix, Vmatrix)
[ LaTeX ] 행렬 표현하기 (matrix, pmatrix, bmatrix, Bmatrix, vmatrix, Vmatrix)
[ LaTeX ] 행렬 표현하기 matrix, pmatrix, bmatrix, Bmatrix, vmatrix, Vmatrix Latex 행렬 표현 6가지 방식 matrix : 괄호 없음 pmatrix : parentheses → ( ) bmatrix : brackets → [ ] Bmatrix :..
supermemi.tistory.com
[ 참고 ]
https://www.math.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf
https://en.wikipedia.org/wiki/List_of_mathematical_symbols_by_subject
반응형
'수학 > Basic' 카테고리의 다른 글
| [ Math ] Convolution(합성곱)의 원리와 목적 (3) | 2021.08.03 |
|---|---|
| [ Math ] Complex Number (복소수) (0) | 2021.07.15 |
| [ Math ] Four-quadrant Inverse Tangent (Arctangent) Function (0) | 2021.07.14 |
| [ 수식, 기호 ] Delta Symbol (델타 : Δ, δ ) (0) | 2021.05.23 |
| 비 유클리드 공간 & 기하학 - 1) hyperbolic geometry(쌍곡 기하학) (2) | 2021.02.08 |



