[ Signal ]Signal Aliasing & Anti-aliasing 에 대하여
앞선글을 읽고 오시면 이해에 도움이 됩니다.
2021.08.06 - [AI/Math] - Sampling Theorem 이란 (Nyquist rate, lowpass filter)
Sampling Theorem 이란 (Nyquist rate, lowpass filter)
앞의 글을 읽고 오시면 이해에 도움이 됩니다. 2021.07.20 - [AI/Math] - Impulses function & Sifting properties Impulses function & Sifting properties 이전글 푸리에 급수 (Fourier Series) 이전글 Complex..
supermemi.tistory.com
Aliasing
Aliasing 이란 잘못된 신호를 의미합니다.
그렇다면 신호 처리에서 aliasing 은 어떤 의미로 사용될까요??
Sampling 후에 신호를 구별할 수 없게 되는 것을 말합니다.
앞선 글에서 설명한 바와 같이 Sampling을 하면 예시 값들로 이루어진 digitized function이 만들어 집니다. 이때 Sampling rate가 낮을경우(Nyquist rate보다 낮을 경우) aliasing이 발생합니다. Aliasing이 존재할 경우, 우리는 원래의 함수가 어떤 모양인지 전혀 알 수 없게 됩니다.
예시를 통해 알아보죠..
Example 1.
fig1. 붉은색 선이 실제 신호라고 합시다. 이때 검은 점은 sampled value입니다. 저 점들을 지나는 신호는 붉은색 실선 말고도 검은색 점선이 존재하지요. 이처럼 sampling rate가 낮으면 원래 신호가 무엇인지 알 수 없게 됩니다. 이런 신호(붉은색 실선, 검은 점선)을 Aliased pair라고 합니다. 이러한 문제 상황을 Aliasing 이라 하지요.

Example 2.
아래 fig 2 그래프들은 이전글 에서 사용된 예시죠.. 다시한번 가져왔습니다.
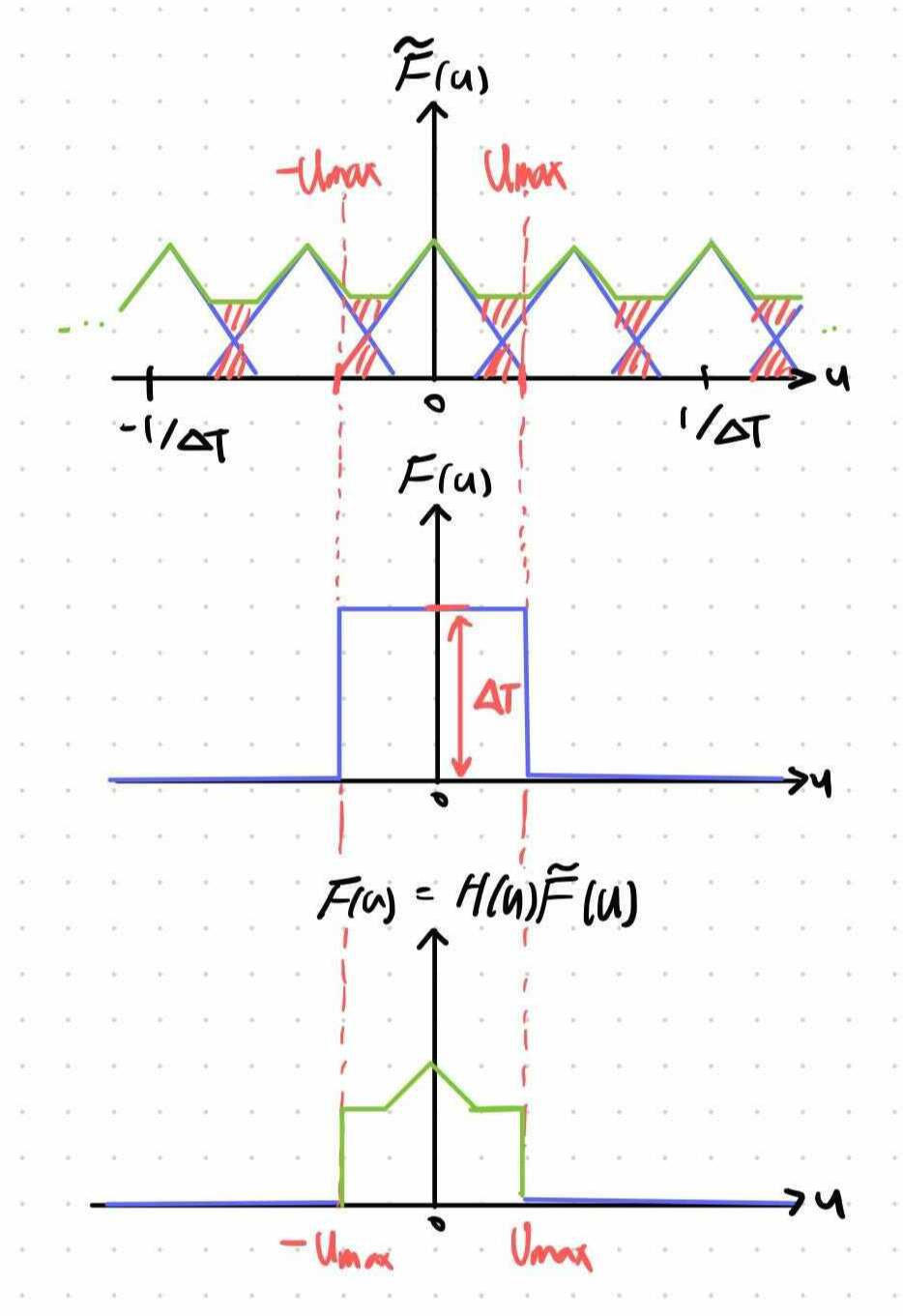
첫번째 그래프는 Fourier transform of under-sampled function 입니다. 두번째 그래프(lowpass filter)을 이용해서 반복되는 하나의 부분(세번째 그래프)만 뽑아냅니다. 문제는 필터를 사용해도 원래의 함수 (파란색 삼각형)을 복원해내지 못한다는 것이지요.
첫번째 그래프에서 보이듯이, 붉은 색 aliasing 영역 때문에 원래의 파란색 함수가 아닌 연두색 함수로 변형되기 때문입니다. 그래서 역푸리에 변환을 하면 원래 함수와 다른 함수가 될겁니다.
Aliasing 은 항상 존재한다?
실제론 항상 aliasing 이 존재할 수 밖에 없습니다.
아날로그 데이터를 푸리에 변환하면 주파수(frequency)가 무한대로 뻗어나가서 작은 값이지만 존재합니다.
아래 유투브 스크린샷 처럼 sampling 하게 되면 aliasing이 발생합니다.

또한 original siganl이 band-limited signal 일지라도 aliasing은 발생합니다.
Signal(function)을 처리하는 과정에서 일반적으로 signal(function)의 duration을 제한합니다.
즉, 제한된 시간동안 기록된(finite interval $t = [0,T]$) signal(function)만 사용하겠다는 의미이지요..
$$ \begin{align} h(t) = \begin{cases} 1 & 0 \leq t \leq T \\ 0 & \text{otherwise} \end{cases} \end{align}$$
$h(t)$ 를 original signal(function) $f(t)$와 곱해주면 쉽게 분리가 됩니다. 이후 푸리에 변환합니다..
Convolution Theorem 을 적용해볼 수 있습니다.
$\mathcal{F}\{ h(t)f(t)\} = F(u) * H(u) ,where\quad * : convolution$
$ F(u)$가 band-limited 이더라도, $H(u)$로 합성곱하게되면 무한대로 뻗어가는 결과를 만들어 냅니다.
즉, 아무리 band-limited 한 function이더라도 duration을 제한하게 되면 더이상 band-limited가 아니게 됩니다..
다시말해, 무한대로 다양한 frequency로 구성되어 있기 때문에 아무리 sampling rate를 높여도 놓치는 부분이 발생하고, aliasing이 발생할 수 밖에 없게 됩니다!!
Anti-aliasing
Sampling rate 향상에도 제한이 있지요. 이를 제외하고 aliasing을 줄이는 다른 방법으로 Anti-aliasing이 있습니다.
Sampling 하기 전 기존 input signal(function)에서 aliasing이 발생하는 높은 주파수(frequency)를 처리하는 과정을 Anti-aliasing이라 합니다. Anti-aliasing을 통해서 aliasing으로 생기는 문제를 줄일 수 있습니다.
간단하게 설명하자면 Anti-aliasing은 Sampling 이전에 filter를 이용해서 aliasing이 발생하는 nyquist rate 바깥쪽을 날려버리는 것이라고 생각하시면 됩니다.
아주 잘 설명되어 있습니다. 제 설명이 부족해서 잘 이해가 안되시는 분은 동영상 보시면 좋을것 같네요.
'수학 > 신호처리' 카테고리의 다른 글
| [ Signal ] Sampling Theorem 이란 (Nyquist rate, lowpass filter) (0) | 2021.08.06 |
|---|---|
| [ Signal ] Sampled Functions의 푸리에 변환 (0) | 2021.08.06 |
| [ Signal ] Function Sampling (샘플링) (1) | 2021.08.05 |
| [ Signal ]푸리에 변환과 합성곱의 관계(Convolution Theorem) (2) | 2021.08.04 |
| [ Signal ] 푸리에 변환 (Fourier Transform) - (2) 다양한 함수의 푸리에 변환 (1) | 2021.07.23 |



