2021/01/28 - [확률과 통계/Probability] - [ 확률과 통계 ] 분산(variance, Var)과 공분산(Covariance, Cor) 이란 - 2
1. 분산의 개념
어떤 확률 변수의 분산(variance, Var) 은 그 확률변수가 기댓값(expected value, E)으로부터 얼마나 떨어진 곳에 분포하는지를 가늠하는 숫자이다.
하나씩 알아보자.
기댓값 (expected value, E)
1) 이산 확률 변수일 경우
x = 사건, p(x) = 사건이 일어날 확률
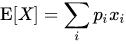
2) 연속 확률 변수일 경우
x = 사건, f(x)는 확률밀도함수
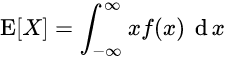
-
기댓값은 선형 연산자이다.
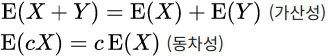
-
정리하자면 기댓값은 어떤 확률적 사건에 대한 '평균' 이라고 생각할 수 있다.
-
이 경우 '모평균(population mean) mu' 으로 다룰 수 있다.
분산 (variance, Var)
앞에서 본 기댓값은 전체 데이터의 평균이라고 생각했을때, 확률변수에서 데이터 위치를 파악할 수 있다.
확률변수 그래프로 보면 기준선이라고 생각하면 편하다.
그렇다면 분산은 어떤 역할을 할까?
분산은 "얼마나 넓게 퍼져 있는가" 를 나타낸다.
아래의 예시를 통해 생각해 보자.
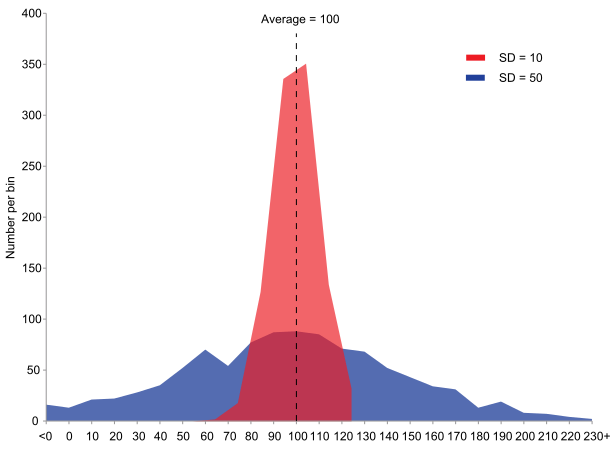
위의 그림은 평균이 같지만 분산이 다른 두 확률 분포를 보여준다.
붉은색 분포를 A, 푸른색 분포를 B 라고할때,
E(A) = 100, Var(A) = 100
E(B) = 100, Var(B) = 2500
푸른색 B의 분산이 더 크고, 분포 또한 더 넓게 퍼져있다.
그렇다면 어떻게 분산을 구할까?
기본적인 식은 다음과 같다.
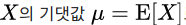
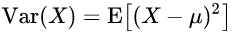
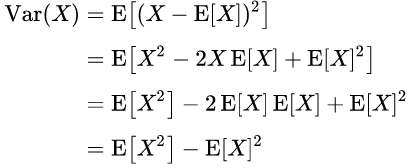
위의 기본적인 식을, 이산확률 변수에서 사용하려면 다음과 같다.
x 사건, p 해당 사건의 발생 확률.

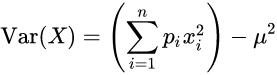
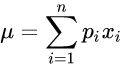
이는 기댓값을 의미한다.
만약 p의 합이 1이 아니라고 한다면, 각 가중치를 총 가중치 합으로 나누어 확률과 같은 성격을 가지도록 조정해야한다.
그런데 만약, 각 해당 사건이 일어날 확률이 모두 같은 상황이라면 어떨까?
주사위의 경우 1/6 로 모든 사건의 발생 확률이 같다. 그럴때는 다음과 같은 식으로 쉽게 분산을 구할 수 있다.
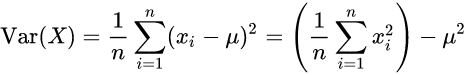
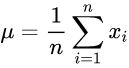
이는 평균값을 의미한다.
만일 확률 변수 X 의 생성 원리가 확률 밀도 함수 f(x)와 누적분포 함수 F(x)를 따르는 연속확률 분포라면, 분산은 다음과 같이 구할 수 있다.
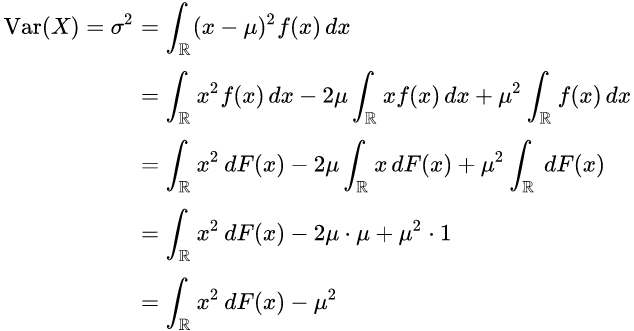
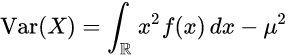
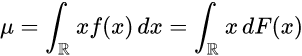
이는 확률 변수 X의 기댓값이다.
공분산의 개념은 다음 글에서 이어서 다루겠다.
2021/01/28 - [확률과 통계/Probability] - [ 확률과 통계 ] 분산(variance, Var)과 공분산(Covariance, Cor) 이란 - 2
[ 확률과 통계 ] 분산(variance, Var)과 공분산(Covariance, Cor) 이란 - 2
앞선 글에서 기댓값과 분산에 대해서 다뤘다. 2021/01/28 - [확률과 통계/Probability] - [ 확률과 통계 ] 분산(variance, Var)과 공분산(Covariance, Cor) 이란 - 1 [ 확률과 통계 ] 분산(variance, Var)과 공분..
supermemi.tistory.com
출처
ko.wikipedia.org/wiki/%EA%B3%B5%EB%B6%84%EC%82%B0
'수학 > 확률 & 통계' 카테고리의 다른 글
| 정규분포 (normal distribution) 란 무엇일까? - 가우시안 분포 (Gaussian normal distribution) (0) | 2021.01.28 |
|---|---|
| 공분산(Covariance, Cor)과 상관계수(Correalation coefficient) 이란 - 2 (2) | 2021.01.28 |
| [ 확률과 통계 ] Total probability & Bayes' Theorem(베이즈 정리) (0) | 2020.04.15 |
| [ 확률과 통계 ] Multiplication rule 과 예제. (0) | 2020.04.15 |
| [ 확률과 통계 ] 이산 균등 확률 & 조건부 확률은 무엇인가? (Discrete Uniform Probability & Conditional probability) (0) | 2020.04.15 |



