앞선 글에서 베이즈 정리를 다루었지만 다시한번 정리해보고자 한다.
2020.04.15 - [확률과 통계/Probability] - [ 확률과 통계 ] Total probability & Bayes' Theorem(베이즈 정리)
[ 확률과 통계 ] Total probability & Bayes' Theorem(베이즈 정리)
이번에 다룰 Total probability 와 Bayes' Theorem을 이해하기 위해서는 기본적인 확률의 규칙들에 대해서 잘 알고 있어야 한다. 앞의 글들을 보고 오길 바란다. 2020/04/15 - [확률과 통계] - [ 확률과 통계 ] M
supermemi.tistory.com
베이즈 정리란?
사전 정보(데이터)를 통해 사후확률(특징이 주어졌을때 판단)을 예측하는 과정에서 사용되는 공식을 말한다.
무슨말인지 도통 이해가 안갈 것이다.
예를 통해 하나씩 정리해 보자.
공항 출입구에 남자와 여자를 판단해주는 프로그램이 있다고 생각해보자.
이때 프로그램은 판단에 있어서 단 하나의 특징(키)만 고려하여 판단한다고 가정하자.

여기서 Class 라는 개념이 나온다.
분류를 위해서는 집단(Class)을 지칭할 필요가 있다.
편의상 남자는 c1, 여자는 c2라고 설정한다.
그리고 하나의 특징(feature) 키정보를 x라고 설정한다.
이때 우리는 지금까지 모은 데이터를 바탕으로 사전정보(Prior probability)를 알고있다.
예를들어, 남자 여자 각각 100명의 키정보 데이터를 통해 사전정보를 알 수 있다.
구체적으로 어떤 사전 정보를 알 수 있을까?
남자일때 키에 따른 확률 = P( x | c1 ) ---> 조건부 확률(conditional probability)
여자일때 키에 따른 확률 = P( x | c2 )
조건부 확률이 무엇인지 모른다면 글을 보고와라.
[ 확률과 통계 ] 이산 균등 확률 & 조건부 확률은 무엇인가? (Discrete Uniform Probability & Conditional probab
기본적인 용어를 잘 모르겠다면 아래의 글을 보고 오길 바란다. 2020/04/03 - [확률과 통계] - 확률의 기본 용어 정리 (experiment, sample space, event, atomic event) 확률의 기본 용어 정리 (experiment, samp..
supermemi.tistory.com
다시 돌아와서, 위와 같이 남자면 키가 어느 정도인지, 여자면 키가 어느정도인지 확률을 알 수 있다.
물론 키가 큰 남자도 있고, 키가 작은 남자도 있을 것이다.
반대로 키카 큰 여자도 있고, 키가 작은 여자도 있을 것이다.
그러나 통계적으로 봤을때 남자의 키가 클것이다.
오류에 대해서는 뒷부분에서 다룰 것이니 지금은 무시하자.
자 그럼 우리는 사전정보(Prior probability)를 알고 있다.
남자일때 키가 클 확률이 크다. 여자일때는 키가 클 확률이 작다.

이때 우리가 알고 싶은 것은 사후확률(Posterior probability)이다.
다시말하면, 공항에 어떤 사람이 들어왔는데 그 사람이 남자인지 여자인지 모른다.
그러나 키가 큰지 작은지 특징은 보이는 상황이다.
이런 상황에서 특징을 통해 그 사람이 남자인지 여자인지 판단하려 할때 베이즈 정리가 사용된다.
다시말해, 사전정보를 통해 사후확률의 판단기준을 정하는 것이다.
앞에서 우리가 알고 있는 사전 정보는 P( x | c1 ), P( x | c2 ) 이다.
우리가 이를 통해 알고 싶은 것은 P( c1 | x ), P( c2 | x ) 이다.
키가 큰 사람을 봤을때 그사람이 남자일 확률을 알고싶은 것이다.
이제 어떤 상황에서 베이즈 정리가 사용되는지 이해했는가?
자 그럼 이제 베이즈 정리가 무엇인지 공식을 알아보자.
베이즈 정리 공식
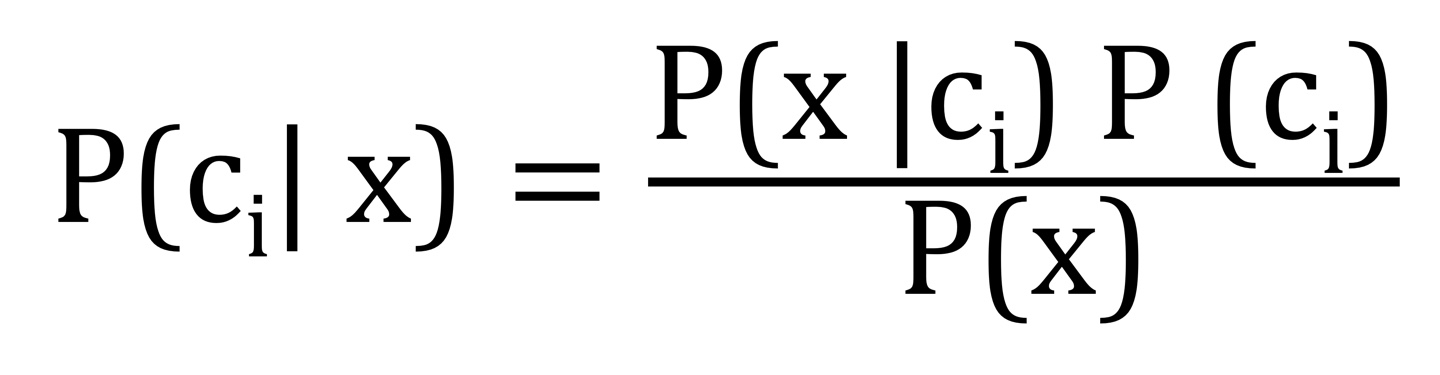
간단히 말하면 우리가 알고싶은 확률 P( c | x )를 구하기 위해,
우리가 아는 확률 P( x | c ), P( c ), P( x )로 이루어진 식으로 바꾸는 것을 베이즈 정리 라고 한다.
위의 식이 성립 되기 위해서는 Class 가 서로 exclusivity & exhaustivity 하다는 조건이 필요하다.
음.. 간단히 말하면 서로 겹치는 것이 없고 전체를 이룬다는 것이다.
다음을 조건 식으로 나타내면 다음과 같이 성립된다.

위의 확률식이 익숙지 않다면 앞의 글을 보고 오는 것을 추천한다.
2020.04.03 - [확률과 통계/Probability] - [ 확률과 통계 ]Probability Laws & Axioms (확률의 규칙)
[ 확률과 통계 ]Probability Laws & Axioms (확률의 규칙)
2020/04/03 - [AI/Math] - 확률의 기본 용어 정리 (experiment, sample space, event, atomic event) 확률의 기본 용어 정리 (experiment, sample space, event, atomic event) 집합과 확률의 관계 집합에 대해서..
supermemi.tistory.com
베이즈 판단
자 이제 우리가 아는 사전 확률 정보를 통해 사후 확률까지 모두 구했다.
그럼 우리는 이제 키가 클때 남자일 확률과 키가 클때 여자일 확률을 알게 되었다.
만약 키가 큰 사람이 보였다고 하면 무엇을 기준으로 판단을 해야할까?
단순히 생각해보면 키카 클때 남자일 확률과 여자일 확률 중 더 높은 확률을 선택하면 되지 않을까?
정답이다.
키가 클때 남자일 확률이 더 높기 때문에 남자라고 판단하는 것이 타당해 보인다.
정리하자면, 베이즈 정리는 사람들의 삶속에서 익숙하게 존재하는 편견을 바탕으로 새로운 사건에 대해서 판단을 내리는 과정을 데이터와 수식을 통해 표현한 것이다.
여기서 하나 더 추가하자면 앞에서 다루지 못한 오류에 대해서 다뤄보자.
만약 키가 커서 남자라고 판단했는데 여자일 경우도 존재한다.
실제로 여자 배구선수들은 남자인 나보다도 키가 훨씬 큰 경우가 많다.
이렇게 잘못 판단한 경우에 그 결과로 비용(risk)이 존재한다.
오류와 비용에 대해서는 다른 예시를 통해 생각해보자.
COVID-19 진단하는 검사 예시이다.
진단검사가 100% 정확하게 바이러스 유무를 판단하면 문제가 없겠지만 실제로는 완벽하지 않다.
COVID를 걸린 사람을 COVID에 걸리지 않았다고 판단할 수도 있고,
COVID를 걸리지 않은 사람을 COVID에 걸렸다고 판단할 수도 있다.
이를 여기서 오류(error)라고 하겠다.
| 실제로 COVID 걸림 | 실제로 COVID 안걸림 | |
| 검사 수치가 높아서 COVID라고 판단 | GOOD (잘 맞췄다) | 재검을 실시하는 비용이 존재하지만, COVID가 아니기 때문에 확산에 대한 우려가 없다. 비교적 적은 비용 |
| 검사 수치가 낮아서 COVID가 아니라고 판단 | 아주아주아주 큰일이다. (오류) 순식간에 전파가 확산될것이다. 오류에 대한 비용이 아주 크다. |
GOOD (잘 맞췄다) |

그러나 오류(error) 중에서도 심각한 비용(risk)이 남는 오류가 있고 비용(risk)이 비교적 적은 오류가 있다.
이때 우리는 진단 검사의 판단기준을 어떻게 해야할까?
비용이 큰 오류에 대해서 민감하게 반응할 필요가 있지 않을까?

그래서 핑크색 새로운 판단기준을 통해 심각한 오류를 줄이는 것이 종합적으로 비용을 줄이게 될 수 있다.
이 과정에서 심각하지 않은 오류가 증가하지만 비용적으로 계산하면 종합 비용은 감소했음을 알 수 있다.
이러한 판단 기준에서 Optimal Decision(가장적절한판단)이 이뤄질 수 있으며, 최적의 판단 기준은 잘못된 판단의 총 비용을 줄이는 방향으로 찾아나간다. (Minimize probability of wrong decision)
이제 그럼 오류에 대한 비용을 실제로 계산 해보자.
COIVD-19 에 걸리지 않은 경우를 c1 이라 하고, 걸린 경우를 c2라고 하자.
COIVD-19 Test result 수치를 특징(feature) x라고 하자.
잠시 생각해보면, 첫번째 예시인 남자 여자판단 예시와 내용만 다를뿐 수식은 동일하다는 것을 알 수 있다.
각설하고 우리가 아는 사전정보는 COVID-19 유무에 따른 검사 수치 정보
P( x | c1 ), P( x | c2 ) 조건부 확률이다.
우리가 알고자 하는 사후확률은 검사 수치가 주어졌을때 실제로 COVID-19에 걸렸을 확률
P( c1 | x ), P( c2 | x ) 조건부 확률이다.
이제 오류 비용에 대해서 알아보자.
비용을 e라고 설정해보면 다음과 같다.
| 실제로 COVID 안걸림(c1) | 실제로 COVID 걸림(c2) | ||
| 검사 수치가 높아서 COVID라고 판단 | e11(good no risk) | e12(serious) | e1 : COVID라고 판단한 결과 비용 |
| 검사 수치가 높아서 COVID가 아니라고 판단 | e21(not serious) | e22(good no risk) | e2 : COVID가 아니라고 판단한 비용 |
e11과 e22는 제대로 맞춘것이기 때문에 거의 0에 가까운 상수가 나온다.
반대로 e21과 e12는 잘못 예측한 오류이기 때문에 비용이 발생한다.
이때 e12 상황은 위에서 말했듯이 심각한 비용을 만들어낸다.
그렇기에 더욱 민감하게 반응해야하고, e12의 값은 다른 비용들보다 큰 숫자가 될 것이다.
e1은 COVID라고 판단한 결과의 총비용이며, e2는 COVID가 아니라고 판단한 결과의 총 비용이다.
e1 = e11 * P( c1 | x ) + e12 * P( c2 | x ) ---- *는 곱셈
비용과 발생할 확률을 곱해줌으로써 상대적인 총 비용을 구할 수 있다.
마찬가지로 e2도 위와 동일한 방식으로 다음과 같이 구할 수 있다.
e2 = e21 * P( c1 | x ) + e22 * P( c2 | x ) ---- *는 곱셈
이때 사후 확률인 P( c1 | x ), P( c2 | x )을 풀어서 오류비용(e)를 구하기 위해 베이즈 정리를 이용한다.
풀이 과정은 직접 해보길 바란다. 그렇게 어렵지 않다.
e1과 e2의 비교를 통해 각 판단에 대한 오류비용이 작은 것으로 판단하는 것이 현명한 선택이 될 것이다.
또한 판단의 기준선을 설정하기 위해서는 총 오류비용이 가장 적은 기준을 찾는것이 중요하다.
이를 위해서는
min(e12 * P( c2 | x ) + e21 * P( c1 | x )) 를 미분하여 최솟값을 찾을 수 있을 것이다.
실제 적용
실제 데이터는 단순히 2개의 class와 1개의 특징 feature로 이뤄져 있지 않다.
훨씬 많은 class와 feature들이 존재하며 모든 것을 고려할 필요가 있다.
이번 글에서 다룬 내용은 매우 기본적인 내용이며 여기서 조금 더 확장하면
3개이상의 class가 존재할 경우?, 2개이상의 feature가 존재할 경우? 를 각각 생각해보고
최종적으로 class와 feature가 다양한 데이터에 대해서 생각해보면 좋을 것 같다.
간단히 말하자면 class가 많아질 경우 대수비교 다항식이 많아질 것이고,
feature가 많아질 경우 conditional joint probability가 되어서 식이 아주 복잡해진다.
그래서 실제로는 feature들이 서로 독립(independent)하다는 가정을 바탕으로 conditional joint probability를 쉽게 풀어쓴다. 이를 " Naive Bayes Classifier " 라고도 한다.
기회가 된다면 추후에 더 다뤄보자.
'수학 > 확률 & 통계' 카테고리의 다른 글
| 다변량 가우시안 정규분포 (Multivariate Gaussian Normal Distribution) (0) | 2021.01.29 |
|---|---|
| 정규분포 (normal distribution) 란 무엇일까? - 가우시안 분포 (Gaussian normal distribution) (0) | 2021.01.28 |
| 공분산(Covariance, Cor)과 상관계수(Correalation coefficient) 이란 - 2 (2) | 2021.01.28 |
| 분산(variance, Var)과 공분산(Covariance, Cov) 이란 - 1 (0) | 2021.01.28 |
| [ 확률과 통계 ] Total probability & Bayes' Theorem(베이즈 정리) (0) | 2020.04.15 |



