[ Signal ] Impulses function & Sifting properties
푸리에 급수 (Fourier Series)
이전글 Complex Number (복소수) 이전글 Four-quadrant Inverse Tangent (Arctangent) Function Four-quadrant Inverse Tangent (4사분면역탄젠트)에 대해서 정리한다 일반적으로 학교에서 sin(사인) cosine(코사..
supermemi.tistory.com
목차
1. Introduction
2. Unit Impulse function (Dirac Delta function; $\delta(t)$)
3. Sifting Property
4. Impulse train ($s_{\Delta T} (t)$)
5. Discrete unit impulse function ($\delta(x)$)
참고자료
1. Introduction
Impulse function & Sifting properties 는 푸리에 변환과 선형 시스템에서 중요한 역할을 한다.
Impulse function의 더 정확한 표현은 distribution 또는 generalized function 이지만, 책이나 강의에서는 impulse function, Dirac delta function 등의 이름으로 사용된다.
2. Unit Impulse Function (Dirac Delta function; $\delta(t)$)
수학자 시메옹 드니 푸아송과 오귀스탱 루이 코시가 푸리에 적분 정리를 연구하면서 처음 고안하였다. 이후 물리학자 폴 디랙이 물리학에서 자주 사용하여 유명해 졌다고 한다. $\large \bf{\delta(t)} $ 로 표기한다

$$\delta(t) = \begin{cases} \infty & \text{if } t=0 \\ 0 & \text{if } t\neq 0 \end{cases} \quad \ldots \quad (1)$$
$$t : \text{continuous variable} $$
$$ \large \int_{-\infty}^{\infty}\delta (t) dt=1 \quad \ldots \quad (2)$$
수식(1) : Unit impulse Function
$ t=0 $ 일때 무한대를 가지며 이를 제외한 나머지 모든 $t$ 에 대해선 0의 값을 가진다. 무한대는 숫자가 아니라 수가 커져가는 상태이기 때문에 명확하게 함수를 정의하기 위해 필요한 제한사항이 있다!
수식 (2) : Unit Impulse Funtion 의 영역은 항상 1 이어야 한다!
이를 근사하는 표현은 매우 다양하다. 그중에 아래 fig 2는 정규 분포를 이용한 근사 표현이다. t = 0 일때 삐죽 spike 가 올라가는 모양이고 영역(area)는 1로 유지된다.

Integrals over Dirac Delta Function Representations - Wolfram Demonstrations Project
This Demonstration compares the integral of a test function multiplying three different representations of the Dirac delta function as the index is increased For each representation The three representations are 1 rectangle 2 Gaussian and 3 Lorentzian The
demonstrations.wolfram.com
Dirac Delta Function(DDF)의 성질
$\large \delta(x) = \delta(-x) $ : 우함수(even function) 이다.

$\delta (ax) = \frac{1}{|a|}\delta (x)$ : 꽤 중요한 성질이니 잘 기억해두자.


3. Sifting Property
우선, " Sift " 라는 단어의 뜻을 아는가?
네이버에 따르면 다음과 같이 "걸러내다", "선별하다" 등의 의미를 가지고 있다

여기서도 비슷한 의미라고 생각하면 된다. Impulse Function은 임의의 다른 함수의 특정값만을 걸러내는 역할(Sifting property)을 한다고 볼 수 있다.
$$ \large \int_{-\infty}^{\infty}f(t)\delta (t) dt=f(0) \quad \ldots \quad (3)$$
수식 (3) : Unit Impulse Function $\delta (t)$ 함수를 임의의 함수 $f(t)$와 곱한 후 적분하게 되면, $t = 0$일때 함수값을 찾아낼 수 있다!

왜냐하면 이론상 $\delta (t)$ 함수는 $\bf{t = 0} $에서만 값을 가지고 나머지 위치에서는 모두 곱셈 결과 0 이되기 때문이다(실제로는 근사하여 범위를 적분). 또한 $\delta (t)$ 함수의 영역을 1로 제한해뒀기 때문에 곱셈하는 $f(t)$ 함수의 $t = 0$의 값은 동일한 크기로 유지가 된다!
그런데 단순히 생각해보면 뭣하러 힘들게 적분하여 값을 구할까? 단순히 $f(t)$ 함수에 0을 대입하면 되는거 아닌가? 라고 생각해볼 수 있다.
사실 Dirac Delta Function은 미분방정식을 푸는 용도로 많이 사용된다

$$ \large \int_{-\infty}^{\infty}f(t)\delta (t-t_0) dt=f(t_0) \quad \ldots \quad (4)$$
수식 (4) : Impulse Function 의 위치가 $t = 0$이 아닌 다른 곳($\bf{ t = t_0}$)일 수 있다. 이 경우 그 위치의$ f(t_0)$ 함수값을 반환한다.
4. Impulse train ($s_{\Delta T} (t)$)
Impulse train 이란 말그대로 Impulse spike가 기차처럼 일정 간격($\Delta T$)을 두고 연속적으로 나타나는 것을 말한다. 머리 빗처럼 동일한 간격으로 솟아 있어서 "Dirac comb" 또는 일정한 간격으로 임의의 함수 값을 sampling 하는 역할도 가능하기 때문에 "Sampling function"이라고도 불린다.
$\large \bf{s_{\Delta T}(t)}$ 로 표기한다.
$$\large s_{\Delta T}(t)= \sum\limits_{k=-\infty}^{\infty}\delta (t-k\Delta T) \quad \ldots \quad (5)$$

Dirac comb - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search periodic distribution ("function") of "point-mass" Dirac delta sampling In mathematics, a Dirac comb (also known as an impulse train and sampling function in electrical engineering) is
en.wikipedia.org
5. Discrete unit impulse function ($\delta(x)$)
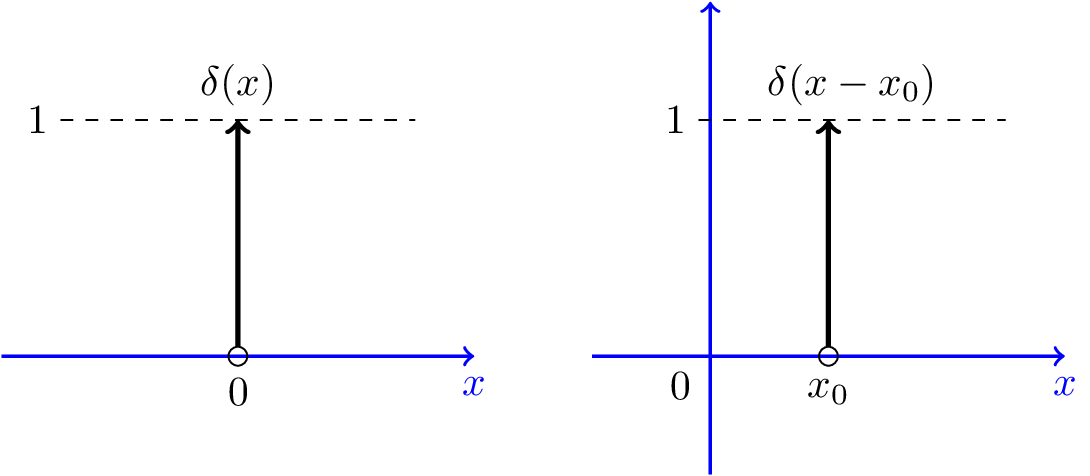
$$\delta(t) = \begin{cases} 1 & \text{if } x=0 \\ 0 & \text{if } x\neq 0 \end{cases} \quad \ldots \quad (6)$$
$$x : \text{discrete variable} $$
$$ \large \sum_{-\infty}^{\infty}\delta (x) dt=1 \quad \ldots \quad (7)$$
$$ \large \sum_{-\infty}^{\infty}f(x)\delta (x) dt=f(0) \quad \ldots \quad (8)$$
$$ \large \sum_{-\infty}^{\infty}f(x)\delta (x-x_0) dt=f(x_0) \quad \ldots \quad (9)$$
수식 (6) : Discrete variable에서는 앞에서 봤던 continuouse variable의 delat function 과 다른점이 한가지 존재한다.
앞에서는 연속 변수 $t = 0$ 일때 $\infty$ 값을 가지도록 이론적으로 설계했지만, 이산 변수 $x = 0$ 일때는 단순하게 1로 정의한다(이를 제외한 나버지 부분은 대부분 동일하다).
수식 (7) : 그래서 당연하게 합은 1이 된다.
수식 (8) : Discrete variable(이산 변수) 에서는 훨씬 이해가 간단하게 된다. 이산 변수를 사용하기 때문에 $x = 0$ 일때만 값을 가지게 되며 즉, delta function(t=0) 값인 1을 $f(0)$에 곱해준 것만 남게된다. 결국 impulse signal 위치에서의 함숫값을 알 수 있다.
수식 (9) : 마찬가지로 impulse signal의 위치를 바꿀 수 있으며, 그 위치에서의 함수 $f(x_0)$ 값을 찾을 수 있다.
Signal train에 있어서도 discrete delta function의 값이 1인 것만 제외하곤 동일하다!
참고자료
디랙 델타 함수 - 위키백과, 우리 모두의 백과사전
델타 함수, 또는 디랙 델타 함수는 수학자 시메옹 드니 푸아송(1815)와 오귀스탱 루이 코시(1816)가 푸리에 적분 정리를 연구하면서 처음 고안하였다. 이후 이론물리학자 폴 디랙이 물리학에서 자
ko.wikipedia.org
디랙 델타 함수(Dirac Delta Function)
물리학, 수학, 전자파, RF, 초고주파, 안테나, 통신 이론, 정보 이론
ghebook.blogspot.com
https://www.youtube.com/watch?v=KreHnRh5h78
'수학 > 신호처리' 카테고리의 다른 글
| [ Signal ] Function Sampling (샘플링) (0) | 2021.08.05 |
|---|---|
| [ Signal ]푸리에 변환과 합성곱의 관계(Convolution Theorem) (2) | 2021.08.04 |
| [ Signal ] 푸리에 변환 (Fourier Transform) - (2) 다양한 함수의 푸리에 변환 (1) | 2021.07.23 |
| [ Signal ] 푸리에 변환 (Fourier Transform) - (1) 기본 유도과정 (4) | 2021.07.21 |
| [ Signal ] 푸리에 급수 (Fourier Series) (1) | 2021.07.17 |



