기본적인 극한의 정의에 대해서 이전의 글에서 다뤘다. 엡실론과 델타를 잘 모르겠다면 앞의 글을 읽고 오길바란다.
2020/03/18 - [AI/Math] - [Math] 극한 (Limit) 이란? (정의와 특성)
[Math] 극한 (Limit) 이란? (정의와 특성)
정의 엡실론 - 델타 논법을 이용하면, 임의의 ε > 0 에 대하여, δ > 0 가 존재하여, 0 < |x - a| < δ 이면 항상, |f(x) - L| < ε 이게 된다. ( if for every number ε>0 the..
supermemi.tistory.com
좌극한과 우극한.
좌극한 우극한은 간단하다. 눈으로 봐도 알 수 있다. 좌극한은 왼쪽에서, 우극한은 오른쪽에서 근사할 때 함수의 값을 말한다.
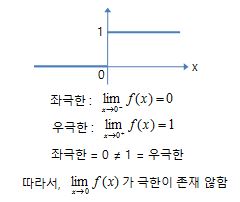
좌극한과 우극한이 존재하며, 좌극한과 우극한이 같을때 우리는 극한이 존재한다고 할 수 있다.
대충 감각적으로 어떤건지는 알 수 있지만, 정확하게 알아야 이후의 연속과 미분에서 제대로 이해할 수 있다.
그렇다면 좌극한과 우극한을 어떻게 정의하고 증명 할 수 있을까?
앞선 글에서 다룬 엡실론-델타 논법을 이용하면 쉽게 설명할 수 있다.
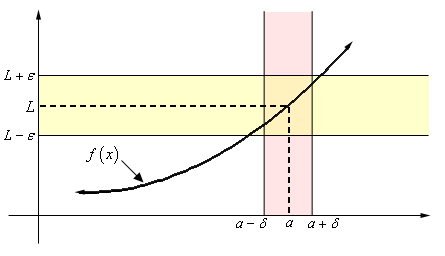
좌극한 일때,
if for every number there exists a number such that
x 가 a 왼쪽에서 접근한다. 그래서 극한의 엡실론-델타 정의와 거의 유사하지만 a−δ < x< a 이 부분만 다르다.
if for every number there exists a number such that
if a < x< a + δ then |f(x)−L| < ε
x 가 a 오른쪽에서 접근한다. 그래서 극한의 엡실론-델타 정의와 거의 유사하지만 a < x< a + δ 이 부분만 다르다.
자세한 증명
http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx
Calculus I - One-Sided Limits
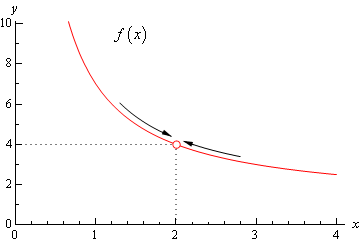
So, as we’ve done with the previous two examples, let’s remind ourselves of the graph of this function. In this case regardless of which side of \(x = 2\) we are on the function is always approaching a value of 4 and so we get, \[\mathop {\lim }\limits_{x
tutorial.math.lamar.edu
http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfLimit.aspx
Calculus I - The Definition of the Limit
In this case both \(L\) and \(a\) are zero. So, let \(\varepsilon > 0\) be any number. Don’t worry about what the number is, \(\varepsilon \) is just some arbitrary number. Now according to the definition of the limit, if this limit is to be true we will n
tutorial.math.lamar.edu
그렇다면 무한대의 극한은 어떻게 정의할까?
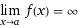
if for every number M there exists a number such that
if 0 < |x - a| < δ then f(x) > M
M : 아주 큰 양수로 정의.
임의의 δ(델타)>0 에 대하여, M > 0가 존재하여, f(x) > M이면
0 < |x - a| < δ then f(x) > M 가 성립한다.
예시 prove that lim x->0 = ∞
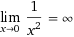
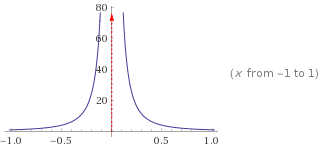
자세한풀이 http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfLimit.aspx
Calculus I - The Definition of the Limit
In this case both \(L\) and \(a\) are zero. So, let \(\varepsilon > 0\) be any number. Don’t worry about what the number is, \(\varepsilon \) is just some arbitrary number. Now according to the definition of the limit, if this limit is to be true we will n
tutorial.math.lamar.edu
출처.
http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfLimit.aspx
http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx
https://ko.wikipedia.org/wiki/%ED%95%A8%EC%88%98%EC%9D%98_%EA%B7%B9%ED%95%9C
https://www.wolframalpha.com/input/?i=%28lim+x-%3E0+1%2Fx%5E2%29
'수학 > Basic' 카테고리의 다른 글
| 미분 공식과 예제 (Chain rule, Power rule, sum/difference rule, Exponential functions, Product rule, Quotient Rule) (0) | 2020.04.12 |
|---|---|
| 함수의 극한, 연속성, 그리고 미분. 기본적인 내용 정리 블로그. (0) | 2020.03.23 |
| 함수의 연속성(continuity)의 정의와 조건(우극한,좌극한) (7) | 2020.03.18 |
| 극한 (Limit) 이란? (정의와 특성) (0) | 2020.03.18 |
| 머신러닝 기초. 쉽게 설명하는 편미분, 체인룰 (2) | 2020.03.12 |



