[ AI 기초 ] 3. Linear Model (classifier)
이전글 : [AI/Series] - [ AI 기초 ] 2. AI 의 역사
[ AI 기초 ] 2. AI 의 역사
[ AI 기초 ] 2. AI 의 역사 이전글 : [ AI 기초 ] 1. Introduction for Artificial intelligence [ AI 기초 ] 1. Introduction for Artificial intelligence [ AI 기초 ] 1. Introduction for Artifi..
supermemi.tistory.com
1. 기호 표기와 문제 정의
DATA SET
- 데이터의 개수 :
- 인덱스 번호 :
- 정답 Label :
Model : Simple Linear Classifier
- Hypothesis
- feature vector 를 입력으로 받아 어떤 출력(output)을 만들어내는 함수
- 모델은 학습 가능한 파라메타(learnable parameter) 세타(
- 보통의 경우 비선형 activation function
- 고전적으로 signed function 을 이용하여 선형 분류기(linear classifier)를 만들 수 있습니다.
- sigmoid activation function을 사용하기도 합니다.
Loss
- 정답이 양수일때, 모델의 결과가 양수이면 곱셈의 결과가 양수가 된다.
- 정답이 음수일때, 모델의 결과가 음수이면 곱셈의 결과가 양수가 된다.
- 위의 loss가 모든 데이터에 대해서 양수가 나오면 모델이 잘 학습했다고 볼 수 있다.
- 반대로 loss가 음수인 데이터가 존재할 경우 여전히 오차가 존재한다고 볼 수 있다.
2. 왜 가중치 벡터

두 벡터의 내적은
이는 기하적인 특성을 잘 나타내 줍니다.
두 벡터의 내적을 두 벡터의 사이 각을 기준으로 생각해 보시죠(이때 벡터는 normalize가 된 벡터라고 생각하세요!)
서로 직교하는 벡터(사이각이 90도)의 내적 결과 = 0
서로 같은 방향을 보고있는 벡터(사이각이 0도)의 내적 결과 = 1
서로 반대 방향을 보고있는 벡터(사이각이 180도)의 내적 결과 = -1

이를 이용하여 입력 특징 벡터(
식에서 가중치 벡터(
벡터의 내적은 정사영(projection)이라고도 생각할 수 있는데, 위의 내적식은 가중치 벡터위로 feature 벡터를 수직으로 정사영한 것의 길이라고 볼 수 있습니다..
그래서 사이 각이 90도가 되는 직교의 경우 정사영했을때 거리가 0이 되므로 벡터의 내적 또한 0이 됩니다.

위와 같이 가중치 벡터(
앞의 벡터의 정의들을 통해 볼때, 붉은 색 선위의 feature vector 와 가중치 벡터를 내적하면 모두 0이 나오게 됩니다.
붉은 선보다 위쪽에 위치하는 어떤 feature vector와 가중치 벡터를 내적하면 양수가 나올 것입니다.
반대로 붉은 선보다 아랫쪽에 위치하는 어떤 feature vector와 가중치 벡터를 내적하면 음수가 나오게 됩니다.
이때 붉은색 선을 결정 경계(Decision Boundary)라고 합니다.
이렇게 결정 경계를 기준으로 방향에 따라 양수와 음수로 구분하게 되는데요.
이를 선형 분류기(Linear Classifier)를 만들 수 있습니다.
3. Bias

붉은색 선을 푸른색 벡터
이때
직선의 방정식 형태로 정리됩니다.
이때
이 두가지
이를 class에 mapping하는 비선형 활성함수를 사용하면 간단한 선형 분류기(linear classifier)가 됩니다.
이때 만들어진
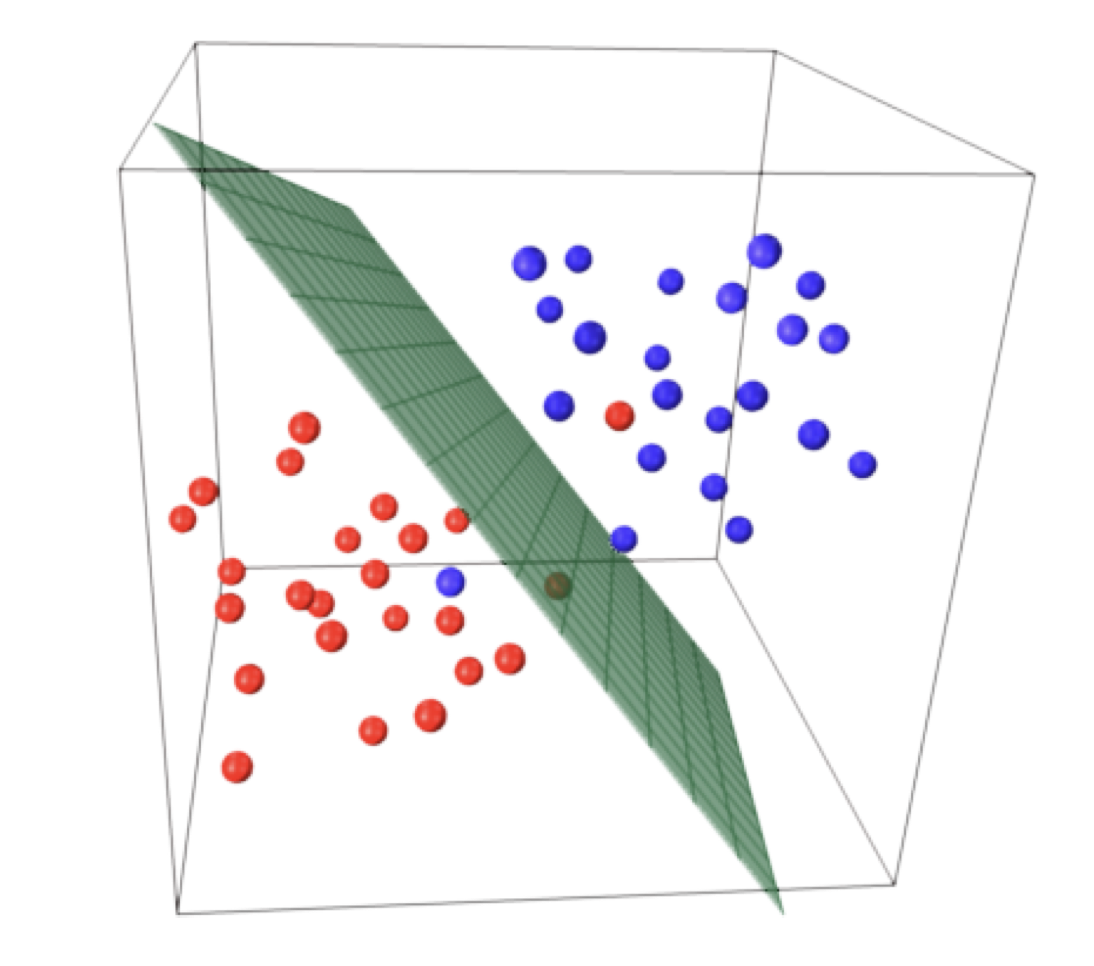
Linear function without offset (through origin)
- Hyperplane =
4. 학습 알고리즘
전체적인 학습과정을 정리하면 아래와 같습니다.
우선 학습가능한 파라메타(Learnable Parameter)를 초기화 합니다.
n개의 데이터를 뽑아서 정의한 모델의 입력값으로 넣어줍니다.
이때 모델의 예측값과 정답 label을 비교하여 loss를 계산하고 오차를 역전파합니다.
역전파를 통해 파라메타를 수정합니다.
이렇게 계속해서 iteration 반복을 돌게 됩니다.
어느정도 학습을 지속하다보면 더이상 크게 변화하지 않는 수준에 도달합니다.
이때 학습을 중지하게 됩니다.

위의 퍼셉트론의 학습알고리즘은 흐름에 따라 직접 예시를 들면서 계산을 해보길 바랍니다.
Set
위에서 loss를 정의했을때 오차를 구했다기 보다 모델이 잘예측하면 +, 예측이 틀리면 -의 값을 가지는 것을 알 수 있습니다.
그래서 조건문을 통해 예측이 틀린 경우에만 update를 실행하게 되구요
update할때는 loss를 각 파라메타 마다 편미분한 다음 이 값을 파라메타에 더해주게 됩니다.
머신러닝 기초. 쉽게 설명하는 편미분, 체인룰
1. 편미분 (partial derivation) 편미분이란 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 생각하여 미분하는 것이다. 간단히 말해, x y 등 다양한 변수가 있는 식에서, 하나의 변수 x 로 미
supermemi.tistory.com
역전파는 정확히 오차의 미분의 반대방향으로 업데이트 해주는 것을 의미합니다.
위의 loss식은 오차가 존재할 경우 부호자체에 마이너스가 곱해져 있어서 그대로 더해줌으로써 update가 가능함을 알 수 있습니다.
식을 직접 한번 차근 차근 보시면 잘 이해가 되실 거에요.
(참고로 위의 경우 초기화를 0으로 했는데 사실 이는 좋은 초기화 방법이 아닙니다. 추후에 좀더 좋은 초기화 방법에 대해서 알아보겠습니다. )
5. 선형 분리(Linearly separable)
만약 어떤 데이터셋이 직선 하나로 분리가 가능하다면 선형 분리(Linearly separable) 가능한 데이터 셋이라고 할 수 있습니다.
즉, 모든 데이터셋에 대해 다음의 식을 만족하는 경우 Linearly separable 하다고 할 수 있습니다.
하지만 실제 세계의 데이터는 단순한 선형 분류기로, 선형 분리가 불가능한 데이터셋이 대부분 입니다.
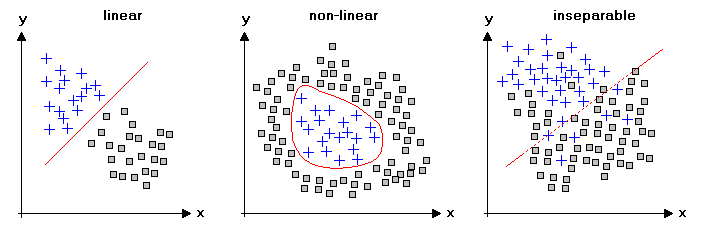
위의 그림을 보면 중간그림과 우측그림은 단순한 하나의 직선으로 완벽한 분리가 불가능하다는 것을 알 수 있습니다.
6. 분류기의 품질 (Classifier Quality)
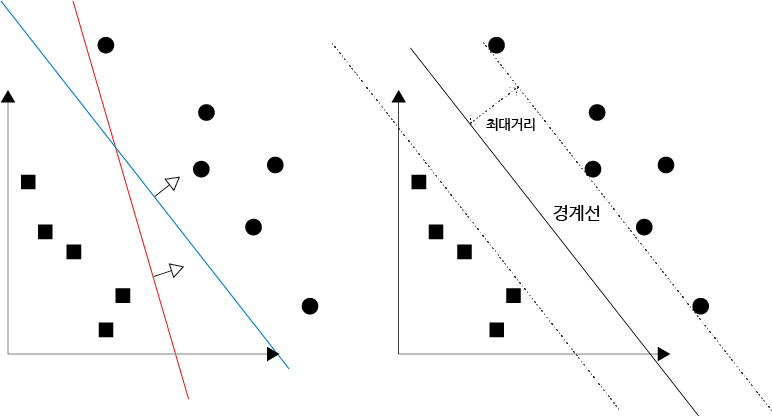
linearly separable한 데이터셋에서 모든 데이터들을 잘 분리하는 직선은 수도 없이 많습니다.
그렇다면 그 직선들 중 가장 좋은 직선은 무엇일까요?
decision boundary와 가장 가까운 데이터 포인트의 최대거리(margin)로 알 수 있습니다.
이 최대거리가 가장 큰 모델이 가장 가장 좋은 선형분리 모델이라고 할 수 있습니다.
데이터 포인트와 decision boundary 사이의 거리(margin)는 어떻게 구할 수 있을까요??
글 앞쪽에서 다룬 벡터 내적의 정사영의 특성을 이용하면 쉽습니다.
어떤 label이 존재하는 데이터 포인트
이식을 통해 각 데이터포인트와의 거리를 측정할 수 있으며, 이를 통해 가장 가까운 데이터 포인트를 찾을 수 있는데요.
이때 찾은 가장 작은 margin을 각 모델들을 비교하여 가장 작은 margin이 클 수록 더 좋은 모델이라고 할 수 있습니다.
7. Training time upper bound
decision boundary가 원점을 지나고, 모든 데이터의 decision boundary와의 최소 거리가 어떤 양수
그리고 모든 데이터 포인트는 어떤 반지름이
이경우 퍼셉트론 알고리즘을 이용하여 학습을 진행했을때, 최대로
다음글 : [ AI 기초 ] 4. Logistic Regression
[ AI 기초 ] 4. Logistic Regression
[ AI 기초 ] 4. Logistic Regression 이전글 : [ AI 기초 ] 3. Linear Model (classifier) [ AI 기초 ] 3. Linear Model (classifier) [ AI 기초 ] 3. Linear Model (classifier) 이전글 : [AI/Series]..
supermemi.tistory.com
'Artificial Intelligence > Basic' 카테고리의 다른 글
| [ Loss ] Cross-Entropy, Negative Log-Likelihood 내용 정리! ( + Pytorch Code ) (1) | 2022.08.21 |
|---|---|
| [ AI 기초 ] 4. Logistic Regression (0) | 2022.04.21 |
| [ AI 기초 ] 2. AI 의 역사 (0) | 2022.04.20 |
| [ AI 기초 ] 1. Introduction for Artificial intelligence (0) | 2022.04.20 |
| Human Pose Estimation 이란? (2022) (0) | 2022.04.04 |



