[ AI 기초 ] 4. Logistic Regression
이전글 : [ AI 기초 ] 3. Linear Model (classifier)
[ AI 기초 ] 3. Linear Model (classifier)
[ AI 기초 ] 3. Linear Model (classifier) 이전글 : [AI/Series] - [ AI 기초 ] 2. AI 의 역사 [ AI 기초 ] 2. AI 의 역사 [ AI 기초 ] 2. AI 의 역사 이전글 : [ AI 기초 ] 1. Introduction for Ar..
supermemi.tistory.com
Classification vs. Regression
이번글에 앞서, classification 과 regression의 차이에 대해 간략하게 알아봅시다.
| Classification | Regression | |
| Input | feature vector \(x \in \mathbb{R}^d\) | feature vector \(x \in \mathbb{R}^d\) |
| Output | Class (ex 개,고양이,..) | Real Number (ex 집값) |
| model | \(h : \mathbb{R}^d \rightarrow {class}\) | \(h : \mathbb{R}^d \rightarrow \mathbb{R}\) |
| Loss | 0-1, asymmetric, NLL | Squared error |
간단하게 정리하면, Classification은 type을 결정하는 분류기 라고 생각하시면됩니다.
Regression 은 어떤 실수값 자체를 예측하는 것이라고 보면 됩니다.
예를들어 보면, classification은 입력데이터가 개인지 고양이 인지 분류하는 것이 목적이고, regression은 입력데이터를 바탕으로 어떤 실수(집값, 주식가격 등)를 직접 예측하는 것입니다.
1. 불확실성을 위한 확률 (Uncertainty)
앞선 글에서도 간략하게 말했지만 완벽하게 linearly separable한 데이터는 세상에 거의 없습니다.
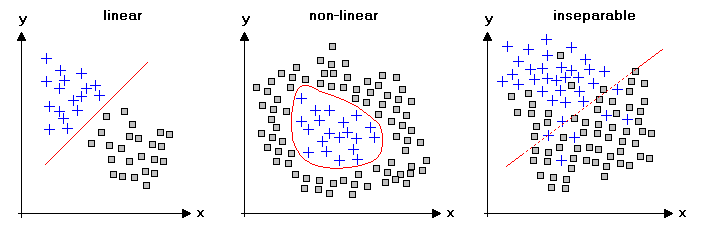
우측의 그림처럼 decision boundary 로 완벽하게 분리되지 않는 데이터의 경우 어떻게 처리할 수 있을까요??
불확실(Uncertainty)한 상황에 대해서 확률의 개념을 적용하면 inseparable data를 학습시킬 수 있습니다.
확률은 말 그대로 사건이 발생할 가능성 정도를 나타냅니다.
예를 들어, '비가올 확률이 50%이다' 라고하면 간단하게 말해 10번 중에 5번은 동일한 상황에서 비가 온다는 것을 의미합니다.
이러한 확률을 나타내는 함수는 여러가지로 나타낼 수 있습니다.
우선 가장 간단하고 많이 쓰이는 시그모이드(Sigmoid) 함수에 대해서 알아봅시다.
2. Sigmoid / logistic function
sigmoid 함수는 다음과 같습니다.
$$\sigma(z) = \frac{1}{1+exp(-z)}$$
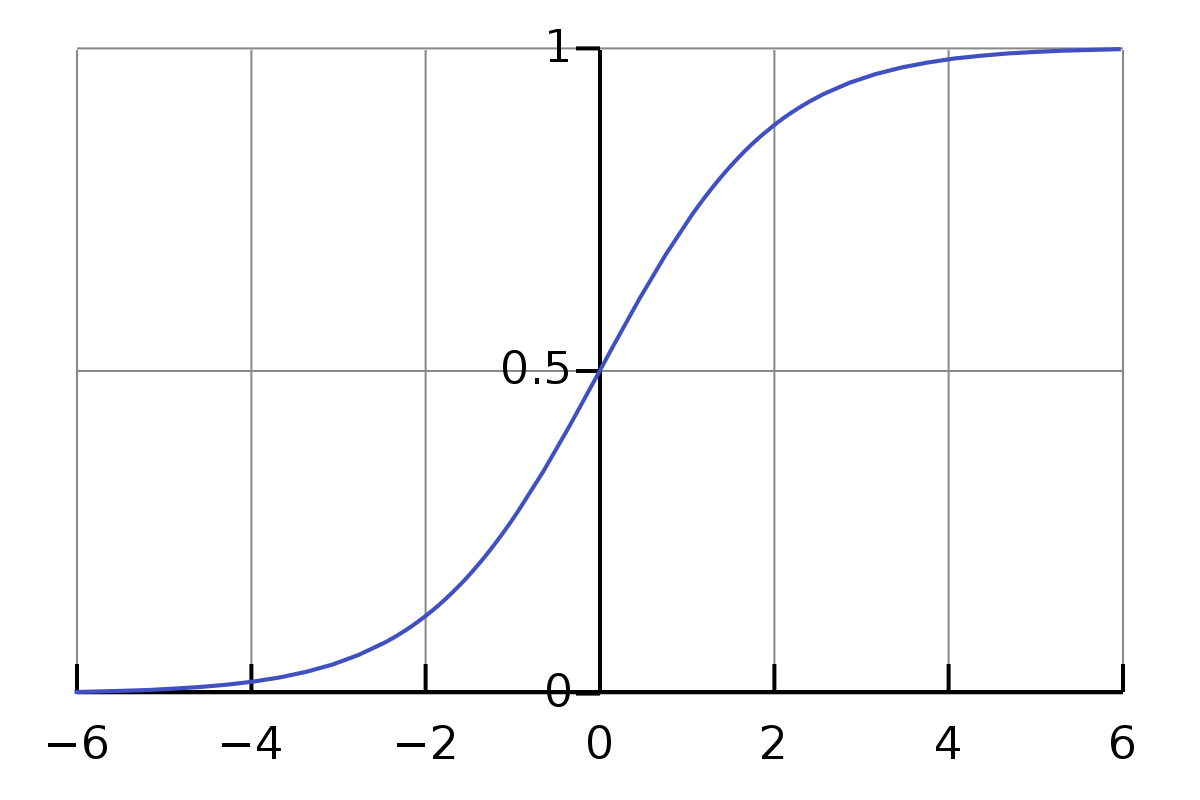
앞글에서 다룬 linear model을 sigmoid function의 input으로 넣어주면 output으로 0~1사이의 확률값을 리턴합니다.
sigmoid함수의 input을 z라고 하겠습니다.
$$\textrm{input } z= h(x) = \theta^T x$$
logistic regression을 이용하여 Binary classification 과제를 해결할 수 있습니다.
확률값 0.5를 기준으로 생각해보죠.
1. 시그모이드 함수 결과가 0.5 보다 클때, 1이라고 분류합니다.
위의 상황을 sigmoid 식을 정리하면 다음과 같습니다.
\(\sigma(\theta^Tx) \gt 0.5\)
\(\frac{1}{1+exp\{-\theta^Tx\}} \gt 0.5\)
\(exp\{-\theta^Tx\} \lt 1\)
\(-\theta^Tx \gt 0\)
앞선 글에서 사용한 linear model과 거의 유사한 모델이 만들어 집니다.
그러나 sigmoid를 적용하면 불확실성을 포착하고, linearly separable하지 않은 데이터셋에서도 제대로된 학습이 가능해집니다.
2. 시그모이드 함수 결과가 0.5 보다 작을때, 0이라고 분류합니다.
이건 어떤 의미일까요?
이전 글에서 벡터 내적의 기하적인 의미를 살펴봤는데요.
/(h(x) = \theta^Tx/) 는 data와 decision boundary간의 거리로 볼 수 있다고 했습니다.
거리가 멀어질 수록 더욱 확실하게 분류 할 수 있겠죠.

그러나 decision boundary 근처에 위치한 데이터일수록 구분하기가 힘듭니다. 이를 확률적인 수치로 판단하자는 겁니다.

보통 gradient descent를 통해 역전파하여 네트워크모델을 학습하게 되는데요.
역전파 과정에서 함수의 미분값을 오차만큼 전파하게 됩니다.
이때 0에 가까운 즉, decision boundary와 가까운 불확실성이 가장 높은 데이터들에 대해서 더욱 민감하게 학습이 진행되게 됩니다.
3. Negative Log Likelihood loss(NLL loss)
이러한 logistic regression(binary classification)문제에 대한 loss로 Negative Log Likelihood loss를 많이 사용합니다.
Cross-Entropy, Negative Log-Likelihood, and All That Jazz
Two closely related mathematical formulations widely used in data science, and notes on their implementations in PyTorch
towardsdatascience.com
구체적인 설명은 위의 글을 참고하시길 바래요!
'Artificial Intelligence > Basic' 카테고리의 다른 글
| [ Loss ] Cross-Entropy, Negative Log-Likelihood 내용 정리! ( + Pytorch Code ) (1) | 2022.08.21 |
|---|---|
| [ AI 기초 ] 3. Linear Model (classifier) (0) | 2022.04.21 |
| [ AI 기초 ] 2. AI 의 역사 (0) | 2022.04.20 |
| [ AI 기초 ] 1. Introduction for Artificial intelligence (0) | 2022.04.20 |
| Human Pose Estimation 이란? (2022) (0) | 2022.04.04 |



