Hungarian Maximum Matching Algorithm 에 대하여 알아보자
이 글을 참고하여 작성하였습니다.
Hungarian Maximum Matching Algorithm | Brilliant Math & Science Wiki
The Hungarian matching algorithm, also called the Kuhn-Munkres algorithm, is a ...
brilliant.org
Hungarian matching algorithm 개요
Kukn-Munkres algorithm 이라고도 불리는 헝가리안 알고리즘은 \(O(|V^3|)\) 의 시간복잡도를 가지고 있습니다.
헝가리안 알고리즘을 통해 Assignment problem(할당문제)인 Bipartite graphs maximum-weight matchings 문제를 빠르게 해결 할 수 있습니다.
여기서 Bipartite graph 는 adjacency matrix 로 표현할 수 있습니다.
- Bipartite_graph : Disjoint and Independent 한 두개의 set을 그래프로 연결한 것
- Adjacency_matrix : 두 정점(vertex)간의 연결(edge)를 나타내는 행렬(matrix), 연결정도를 weight를 통해 나타낼 수도 있음

Hungarian matching algorithm 이 풀고자 하는 문제 정의
Complete bipartite graph 에서, maximum-weight matching 을 찾는 것!
- Complete_bipartite_graph : 같은 집단(subset) 안의 정점(vertex)끼리의 연결이 없으며, 다른 집단(subset)의 정점(vertext)간에는 가능한 모든 연결이 있는 그래프를 말함.
- Maximum_weight_matching : 연결(edge)의 weight가 존재하는 그래프에서, 연결(matching)했을때 모든 weight의 합산이 큰 연결 방식(Matching)을 찾는 것이다. 다시말해, 어떻게 연결해야 최대한의 이익이 나오느냐에 대한 문제로 생각할 수 있다. 동일한 방식으로 Minimum-weight matching (최소 비용 연결 문제)로 치환 할 수도 있다.
- Assignment_problem : Bipartite graph 에서의 maximum-weight matching 은 할당 문제(Assignment problem)이 된다. 이는 실생활에서 다양하게 적용된다.
예를 들어 생각해 보자.
당신이 결혼 10주년 파티를 열려고 한다.
파티에는 노래와 음식이 빠질 수 없다.
또한 파티가 끝난 후 정리하는 비용도 생각해 봐야 한다.
직접 준비하려니 귀찮다 회사를 통해 돈을 써서 파티를 열어보자!!
여러 파티 회사들이 존재한다. (Company A,B,C)
각 회사들은 음악, 요리, 정리에 대해 각각 서비스를 제공하는데 가격이 다르다.
각 항목별로 어떤 회사를 선택해야 최소한의 비용으로 파티를 할 수 있을까?
이때 각 항목별로 하나의 선택만 가능하다.

(가능한 모든 조합 경우의 수를 고려하는)Brute Force 방법을 사용하면 최적의 값을 찾을 수 있다.
하지만 선택지(n)가 많아지면 그에 따른 조합도 엄청나게 늘어나서 비효율적이다 → \(O(n!)\)
이를 \(O(|V^3|)\) 의 시간복잡도로 좀 더 효율적이고 빠르게 해결하는 알고리즘이 Hungarian Algorithm 이다.
The Hungarian Algorithm Using an Adjacency Matrix
우선, Adjacency Matrix 를 이용한 헝가리안 알고리즘에 대해 알아보자.
헝가리안 알고리즘에 적용되는 핵심 아이디어는 다음과 같다.
Cost matrix에서 row, column 방향으로 값을 빼거나 더한 후 최적의 연결(optimal matching)을 찾는 것은 Original Cost matrix에서 최적의 연결을 찾은 결과와 동일하다!!
즉, 쉽게 설명하면 복잡한 숫자로 이루어진 Adjacency matrix를 쉽게 변형해서 최적의 선택이 무엇인지 알기 쉽게 만든 후 선택하자는 것이다.
진행 과정을 통해 자세히 알아보자!!
Step 1. 각 행(row)에서 최솟값을 구한 후 빼준다.

예시 행렬을 보자.
첫번째 행에서 최솟값은?? 108
두번째 행에서 최솟값은?? 135
세번째 행에서 최솟값은?? 122
각 행의 요소들에서 최솟값을 빼준다. 그결과 다음과 같이 나온다.

Step 2. 각 열(column)에서 최솟값을 구한 후 빼준다.
Step 1 의 결과로 나온 예시 행렬에서
첫번째 열에서 최솟값은?? 0
두번째 열에서 최솟값은?? 0
세번째 열에서 최솟값은?? 40
각 열의 요소들에서 최솟값을 빼준다. 그결과 다음과 같이 나온다.

Step 3. 0을 가장 많이 포함하는 행 또는 열을 최소 개수로 찾아준다.
검은색 영역이 step 3에서 찾은 라인이 된다.

Step 4.
만약 찾은 라인의 개수 == n, Go to step 6
만약 찾은 라인의 개수 < n, Go to step 5
우리의 예시 행렬은 n = 3 이다.
그러나 step 3의 결과로 찾은 라인이 2개이다. 그래서 step 5로 이동한다.
Step 5.
5-1) step 3. 에서 찾은 라인으로 covered 되지 않은 elements 중 최솟값을 찾는다.
5-2) Crossed out 이 아닌 row에 최솟값을 빼준다. (다시말해, 이미 찾은 optimal row line 에는 변화를 주지 않는다는 의미)
5-3) Crossed out column 에 최솟값을 더해줘서, 마이너스 부분을 다시 0으로 바꿔준다.(다시말해, 이미 찾은 optimal column line 에는 변화를 주지 않는다는 의미)
5-4) Go back to step 3.
5-1) 우리의 예시 → 라인으로 커버 되지 않는 영역(흰색)에서 최솟값은 2가 된다.
5-2) Crossed out 이 아닌 첫번째, 세번째 row에서 최솟값 2를 빼준다.

5-3) 마이너스 부분을 상쇄시키기 위해 Crossed out 된 첫번째 column 에 최솟값 2를 더해준다.
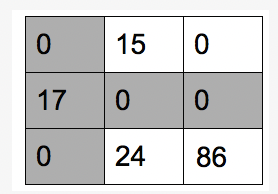
5-4) step 3 로 돌아가 다시 0를 최대한으로 가지는 row 또는 column을 최소 개수로 찾는다.
총 3개의 라인이 찾아졌음으로 Go to step 6를 실행한다.

Step 6.
6-1) 각 row와 column에서 하나의 0만 가지는 조합을 찾는다.
6-2) Original matrix에서 찾은 최적 조합의 위치를 적용한다.
6-1) 예시에서는 총 5개의 0이 존재한다.
선택 후보 : {(1,1),(1,3),(2,2),(2,3),(3,1)}
찾은 선택 : {}
최적의 매칭(3개)을 찾아내는 문제로 바뀐다.

먼저, 세번째 행(row 3)에서는 첫번째 열(column 1)일때만 0을 갖는다. 따라서 (3,1)은 무조건 선택해야 한다.
선택 후보 : {(1,1),(1,3),(2,2),(2,3)}
찾은 선택 : {(3,1)}
(3,1)이 선택 되었기 때문에 첫번째 열(column 1)에서는 다른 선택이 있을 수 없다.
따라서 (1,1)은 후보에서 제외된다.
선택 후보 : {(1,3),(2,2),(2,3)}
찾은 선택 : {(3,1)}
(1,1)이 후보에서 사라졌기 때문에 첫번째 행(row 1)에서는 (1,3)만 남게 된다.
따라서 (1,3)을 선택한다.
선택 후보 : {(2,2),(2,3)}
찾은 선택 : {(1,3),(3,1)}
(1,3)이 선택 되었기 때문에 세번째 열(column 3)에서는 다른 선택이 있을 수 없다.
따라서 (2,3)은 후보에서 제외된다.
선택 후보 : {(2,2)}
찾은 선택 : {(1,3),(3,1)}
최종적으로 남은 위치를 선택해 준다.
선택 후보 : {}
찾은 선택 : {(1,3),(2,2),(3,1)}

Original matrix에 위치를 대입해보면 다음과 같다.
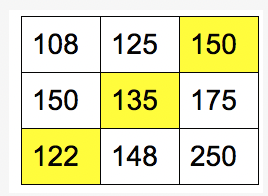
최종적인 비용은 : 407$ 가 된다.
찾은 조합이 최선의 조합인지 확인해 보자.
Brute Force 로 찾은 모든 조합의 결과는 아래와 같다. (n! 조합의 수)

헝가리안 알고리즘의 결과가 최적의 조합임을 알 수 있다!!
The Hungarian Algorithm Using a Graph
또한, 헝가리안 알고리즘은 Bipartite graph의 weight를 이용하여 적용할 수 있다!
이 과정은 perfectly match된 그래프의 Feasible labeling을 찾으면 얻을 수 있다.
- perfect matching 이란 그래프의 모든 정점(vertex)이 각자 하나의 연결(edgd)에만 사용되고, 모든 정점(vertex)이 어떤 임의의 연결(edge)에 사용된 상태를 의미한다.
[그래프] Feasible labeling 이란? (Graph labeling)
Feasible labeling 이란? 우선, 라벨링 한다는 것은 어떤 의미 일까요? (Labeling) 임의로 객체를 구별할 수 있는 무엇인가를 부여한다는 의미입니다. 예를 들어서, 딥러닝에서 학습하기위해 사용하는
supermemi.tistory.com
-
[핵심 아이디어]
Graph 의 Perfect match 에 대한 Feasible labeling 의 결과는 maximum-weighted matching 과 동일한 결과를 만들어 낸다.
[핵심 아이디어 증명]
두 정점(vertex)를 연결하는 연결(edge)를 e라고 하자.
모든 정점(vertex) v 는 각각 한번씩만 사용된다.
이러한 가정 하에서 다음의 inequality 성질을 가지게 된다.
\(w(M') = \sum\limits_{e \in E} w(e) \leq (l(e_x)+l(e_y))=\sum\limits_{v \in V}l(v), \)
\(M'\) : 정점들(vertices)의 랜덤 할당으로 만들어진 임의의 perfect maching 을 의미한다.
\(l(x)\) : Numeric label to node x
위의 식이 의미하는 것은 \(\sum\limits_{v \in V}l(v), \) 가 임의의 perfect matching 비용에 대한 upper bound 가 된다는 것이다.
즉, \(M\) 을 perfect match 라고 할때,
\(w(M) = \sum\limits_{e \in E} w(e)= \sum\limits_{v \in V}l(v), \) 라고 정의 할 수 있는데,
\(w(M') \leq w(M) \) 로 정리할 수 있다.
결국 이때의 \(M\)이 optimal 한 선택이 된다.
작성중...
'소프트웨어자료 > 자료구조 & 알고리즘' 카테고리의 다른 글
| [그래프] Feasible labeling 이란? (Graph labeling) (0) | 2022.04.12 |
|---|---|
| Linked list (연결 리스트) 란 무엇인가? (0) | 2020.05.21 |
| [자료구조] 순환 알고리즘 (이원 탐색, 순열 생성) (0) | 2020.04.13 |
| [자료구조] Binary search (with Recursion(재귀) pseudo code) 예제. (0) | 2020.03.17 |
| [자료구조] Selection Sort ( with pseudo code) 해보기. (0) | 2020.03.16 |



